38. Тесты и задачи 6

(В – Верно, Н – Неверно)

1. В бескоалиционных играх могут рассматривать конфликты двух и более игроков.

2. В бескоалиционных играх могут рассматриваться конфликты только с нулевой суммой.

3. Конечная бескоалиционная игра двух игроков с ненулевой суммой называется биматричной игрой.

4. В бескоалиционных играх принцип максимина не всегда является принципом, по которому находится решение игры.

5. Ситуация в бескоалиционной игре, приемлемая для всех игроков, называется ситуацией равновесия (оптимальной по Нэшу).

6. В бескоалиционных играх как оптимальные следует квалифицировать не действия того или иного игрока, а совокупность действий всех игроков.

7. В бескоалиционной игре решение игры – это, чаще, нахождение ситуаций равновесия.

8. Игроку в бескоалиционной игре может быть выгодным информировать противника о своей стратегии.

9. В оптимальной по Парето ситуации игроки могут совместными усилиями увеличить выигрыш какого-либо из игроков, сохранив выигрыши всех остальных игроков.

10. Ситуации равновесия не отличаются от ситуаций оптимальных по Парето.

11. Ситуации оптимальные по Парето находить труднее, чем ситуации равновесия в той же бескоалиционной игре.

12. В бескоалиционной игре кооперация игроков может быть им выгодна.

13. В теореме Нэша утверждается, что в каждой бескоалиционной игре существует хотя бы одна ситуация равновесия.

14. Любая конечная бескоалиционная игра имеет конечное и четное число ситуаций равновесия.

15. Метастратегия понимается как способ выбора игроком J своей стратегии в зависимости от получаемой им информации о стратегии, выбираемой игроком K.

16. Каждая конечная бескоалиционная игра двух лиц имеет в своей первом метарасширении ситуации равновесия.

17. Каждая конечная бескоалиционная игра двух лиц имеет в своей третьем метарасширении ситуацию, которая является одновременно ситуацией равновесия и оптимальной по Парето.

Задачи

І. Найти ситуации оптимальные по Парето и ситуации устойчивые по Нэшу для следующих биматричных игр:

1.

2.

3.

4.

5.

6.

7.

8.

ІІ. Решить бескоалиционную игру “Экологический конфликт”.

Формулировка игры. Два промышленных предприятия (А и В), расположенные вблизи обширного водоема, берут из него воду для технических нужд и после использования сбрасывают ее обратно в водоем. Если суммарный объем сбрасываемой (загрязненной) воды не превышает некоторого предела d, то происходит ее естественное очищение, и общий водный ресурс сохраняется. Если же указанный предел нарушен, то загрязненность водоема интенсивно растет. Возникает проблема его восстановления за счет предприятий и уплаты штрафов, общая стоимость чего составляет Q.

Чтобы избежать неприятных последствий, приходится строить очистные сооружения, состоящие из отдельных стандартных блоков, рассчитанных на определенные объемы пропускаемой через них воды (пусть каждый блок восстанавливает 25% используемой воды). Затраты на приобретение, монтаж и эксплуатацию одного блока равны С.

Суть конфликта, возникающего между предприятиями, сводится к их стремлению обеспечить себе благоприятные условия деятельности путем более свободного расходования природной воды. Это отрицательно влияем на состояние источника и через него – на ход производства, качество продукции обоих предприятий. Все оказывается взаимосвязанным, и появляется заинтересованность в поиске решений, приемлемых для конфликтующих сторон, хотя никакой договоренности между ними не предусматривается.

Математическая модель. Данный конфликт можно представить как бескоалиционную игру двух лиц следующим образом.

Пусть количество воды, потребляемой каждым предприятием в его технологическом цикле равно единице (100 т, 10 цистерн, и т. д.). Количество очищаемой воды составляет 1 – Х на предприятии А; 1 – Y на предприятии В, где чистые стратегии игрока А = |0; 0,25; 0,5; 0,75; 1|, в зависимости от числа применяемых очистных блоков. Чистые стратегии игрока В = |0; 0,25; 0,5; 0,75; 1|.

Расходы предприятия А составляют:

4С(1 – Х), если Х + У £ d;

4С(1 – Х) + Q, если Х + У > d,

А расходы предприятия В –

4С(1 – У), если Х + У £ d;

4С(1 – У) + Q, если Х + У > d.

Данные формулы позволяют составить платежные матрицы игроков А и В. Для случая имеем

В А	В4	В3	В2	В1	В0
А4	4С 4С	4С 3С	4С+Q 2С+Q	4С+Q С+Q	4С+Q Q
А3	3С 4С	3С+Q 3С+Q	3С+Q 2С+Q	3С+Q С+Q	3С+Q Q
А2	2С+Q 4С+Q	2С+Q 3С+Q	2С+Q 2С+Q	2С+Q С+Q	2С+Q Q
А1	С+Q 4С+Q	С+Q 3С+Q	С+Q 2С+Q	С+Q С+Q	С+Q Q
А0	Q 4С+Q	Q 3С+Q	Q 2С+Q	Q С+Q	Q Q

Индекс при чистых стратегиях игроков указывает на количество используемых очистных блоков (например А3 – предприятие А использует 3 очистных блока; В0 – предприятие В не использует ни одного очистного блока).

Найти ситуации оптимальные по Парето и ситуации равновесия по Нэшу при следующих исходных данных:

9. С >> Q; 10. С << Q;

11. 5С = Q; 12. 5С = Q; ;

13. 4С = Q; ; 14. 2С = Q; ;

15. 2С = Q;; 16. С = 3Q; ;

17. С = 2Q; ; 18. С = Q; ;

19. С = Q; ; 20. С = 4Q; .

ІІІ. Найти множества всех ситуаций оптимальных по Парето в следующих биматричных играх:

21.

22.

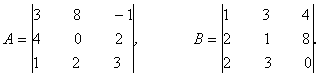
23.

24.

25.

26.

27.

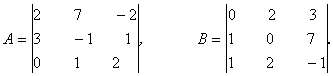
28.

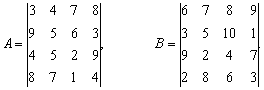
< Предыдущая		Следующая >