14. Решение игр 2xn и mx2
Как уже отмечалось в теореме об активных стратегиях, любая конечная игра Mxn имеет решение, в котором число активных стратегий каждого игрока не превосходит![]() , где
, где ![]() . Следовательно, у игры 2xn или Mx2 всегда имеется решение содержащее не более двух активных стратегий у каждого из игроков
. Следовательно, у игры 2xn или Mx2 всегда имеется решение содержащее не более двух активных стратегий у каждого из игроков ![]() . Если эти активные стратегии игроков будут найдены, то игры 2xn и Mx2 превращаются в игры 2x2, методы решения которых рассмотрены выше.
. Если эти активные стратегии игроков будут найдены, то игры 2xn и Mx2 превращаются в игры 2x2, методы решения которых рассмотрены выше.
Практически решение игры 2xn осуществляется следующим образом:
1) строится графическое изображение игры для игрока А;
2) выделяется нижняя граница выигрыша и находится наибольшая ордината нижней границы (максимин), которая равна цене игры V;
3) определяется пара стратегий игрока В, пересекающихся в точке оптимума. Эти стратегии и являются активными стратегиями игрока В.
Таким образом, игра 2xn сведена к игре 2x2, которую более точно можно решить алгебраическим методом.
Если в точке оптимума пересекается более двух стратегий, то в качестве активных стратегий может быть выбрана Любая пара из них.
Решение игры Mx2 осуществляется аналогично. Но в этом случае строится графическое изображение игры для игрока В и выделяется не нижняя, а верхняя граница выигрыша (так как находится оптимальная смешанная стратегия игрока В), и на ней находится точка оптимума с наименьшей ординатой (минимакс).
Пример. Найти решение игры, платежная матрица которой имеет вид:
|
Ai |
B1 |
B2 |
B3 |
|
A1 |
2 |
5 |
8 |
|
A2 |
7 |
4 |
3 |
Платежная матрица не имеет седловой точки, поэтому оптимальное решение должно быть в смешанных стратегиях. Строим графическое изображение игры для игрока А (рис.2.10)
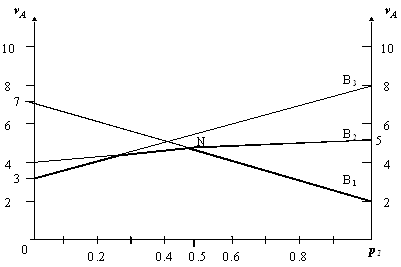
Рис. 2.10
Точка N (максимин) является точкой оптимума. В этой точке пересекаются линии, соответствующие активным стратегиям В1 и В2 игрока В. Таким образом, исключая стратегию В3, получаем матричную игру 2x2 с платежной матрицей вида
|
Ai |
B1 |
B2 |
|
A1 |
2 |
5 |
|
A2 |
7 |
4 |
Используя алгебраический метод решения этой игры, получаем точное решение
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() .
.
Ответ: ![]() ;
; ![]() ;
; ![]() .
.
Пример. Найти решение игры, платежная матрица которой имеет вид
|
Ai |
B1 |
B2 |
|
A1 |
0 |
1 |
|
A2 |
4 |
2 |
|
A3 |
-1 |
4 |
|
A4 |
1 |
-3 |
|
A5 |
6 |
-2 |
|
A6 |
1,5 |
3 |
Платежная матрица не имеет седловой точки. Для сведения данной игры к игре 2x2 строим ее графическое изображение для игрока В (рис. 2.11).
Точка М (минимакс) является точкой оптимума. В этой точке пересекаются отрезки, соответствующие активным стратегиям А2, А6 и А3 игрока А. Таким образом, исключая стратегии А1, А4 и А5 и выбирая из трех активных стратегий две (например, А2 и А3 или А2 и А6), приходим к матричной игре 2x2. Выбор стратегий А3 и А6 исключен, так как в этом случае точка М перестанет быть точкой минимакса.
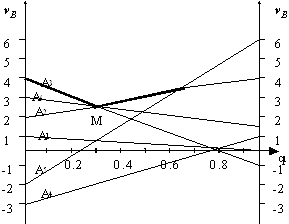
Рис.2.11
Пусть выбираются стратегии А2 и А3. Тогда игра 2x2 приобретает вид
|
Ai |
B1 |
B2 |
|
A2 |
4 |
2 |
|
A3 |
-1 |
4 |
Оптимальные смешанные стратегии данной игры, а, следовательно, и исходной игры определяются следующими вероятностями:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() .
.
Ответ: ![]() ;
; ![]() ;
; ![]() .
.
Другой вариант игры 2x2 получается, если использовать стратегии А2 и А6. В этом случае платежная матрица имеет вид
|
Ai |
B1 |
B2 |
|
A2 |
4 |
2 |
|
A6 |
1,5 |
3 |
Тогда
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() .
.
Ответ: ![]() ;
; ![]() ;
; ![]() .
.
Естественно, что цена игры для обоих вариантов одинакова.
В заключение наметим общую схему решения матричных игр 2xn и Mx2:
1. Определяется наличие седловой точки, т. е. возможность решения игры в чистых стратегиях. Если нижняя цена игры A не равна верхней цене игры B, то осуществляется поиск решения в смешанных стратегиях.
2. Производится упрощение матричной игры путем исключения дублирующих и доминируемых стратегий. Если упрощенная игра имеет размерность не 2x2, то переходим к этапу 3.
3. Строится графическое изображение игры и определяется две активные стратегии игрока, имевшего в исходной задаче число стратегий больше двух.
4. Решается матричная игра 2x2.
| < Предыдущая | Следующая > |
|---|