17. Формальные степенные ряды и действия над ними. Производящие функции последова-тельностей

Пусть - числовая последовательность; Формальный степенной ряд - это символ вида , в котором числа называют-ся Коэффициентами, а символ называется Переменной. Фрагменты степенного ряда называются Слагаемыми; когда коэффициент , слагаемое , т. е. записывать необязательно. Любой многочлен можно считать записью формального степенного ряда, в котором все коэффициенты, начиная с какого-то номера, равны нулю.

Вместо символа часто пишут символ . Два формальных степенных ряда и считаются Равными, если для каждого выполняется равенство:

Над формальными степенными рядами определяется некоторые действия, являющиеся обощением арифметики многочленов.

Сложение. Пусть

Два формальных степенных ряда от одной и той же переменной ; Сложением этих рядов называется действие, в результате которого возникает третий формальный степенной ряд , называемый Суммой рядов и , такой, что

Таким образом, . Нетрудно проверить, что для любых трех формальных степенных рядов имеет место равенство:

А для любых двух формальных степенных рядов справедливо равенство:

Из сказанного следует, что формальный степенной ряд играет в определенном только что сложении роль нуля. Кроме того, если - формальный степенной ряд, то ряд играет роль Противоположного элемента: .

Вычитание. Если

- два формальных степенных ряда, то ряд , получаемый по пра-вилу , называется Разностью, а действие, создающее разность, назы-вается Вычитанием. Очевидно, что вычитание - это прибавление противоположного ряда.

Умножение. Пусть

Два формальных степенных ряда; построим третий формальный степенной ряд , который будет называться Произведением Рядов и , а действие, приводящее к произведению, будет называться Умножением:

Для умножения сохраняется традиционная символика: произведение рядов и записывается в виде . Ясно, что для любых трех рядов справедливы равенства:

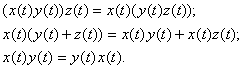
Ряд обладает, очевидно, тем свойством, которое присуще в числовом умноже-нии единице: для любого формального степенного ряда имеет место равенство: . Если для некоторых двух формальных степенных рядов и выпол-няется равенство , то эти ряды называются Обратными по отношению к друг другу. Пишут

Деление. Это действие, которое по двум формальным степенным рядам

При обязательном предположении - - создает третий ряд такой, чтобы оказалось выполненным равенство: . Расписываем последнее равенство по коэффициентам:

следовательно ;

.................................................................

следовательно ;

...........................................................................................

Ряд называется Частным от деления Ряда

На ряд ; часто пишут: .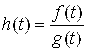

Заметим для примера:

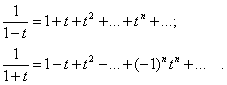
И последнее определение. Формальный степенной ряд называется Производящей функцией Последовательности . Действия над формальными степенными рядами, определенные выше, это - и действия над производящими функциями.

Пример использования техники действий над производящими функциями будет приведен в следующей лекции.

< Предыдущая		Следующая >