16. Метод включения-исключения перечисления элементов множества, не обладающих заданными свойствами. Задача о беспорядках и задача о встречах

Существует классический способ описания элементов некоторого множества с некото-рыми особенностями, который называется Методом включения-исключения. Сформулируем соответствующую задачу.

Пусть - некоторое (как обычно, конечное) множество и - список свойств, которыми могут обладать и не обладать элементы из . Требуется указать формулу, выражающую количество элементов, не обладающих ни одним из свойств заданного списка, через какие-либо вычисляемые величины.

Описываемый ниже способ решения называется Методом включения-исключения. Пусть символ обозначает количество элементов множества , обладающих свойст-вами из . Искомое количество элементов обозначим через ;

Количество элементов в обозначим через . Можно доказать, что имеет место следующая формула (ее так же называют Формулой включения-исключения):

Где суммирование производится по всевозможным сочетаниям свойств из множества : в первом случае - по сочетаниям по одному свойству, во втором случае - по сочетаниям по два свойства и так далее, в -ом случае - по сочетаниям по свойств.

Мы разберем эту формулу подробнее на двух примерах. Первый из них называется Задача о беспорядках. Рассматриваются всевозможные перестановки на символах. Как известно, их общее количество равно . Будем с каждой перестановкой символов

связывать матрицу

,

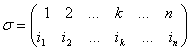Которая называется Подстановкой ; принято говорить, что Подстановка S переводит элемент в элемент , элемент в элемент , ...,элемент В элемент ,... элемент в элемент . Пишут: , Если , то говорят, что подстановка S оставляет Элемент На месте. Подстановка, в которой на месте не остается ни один элемент, называются Беспорядком. При , например, нетрудно перечислить все подстановки вообще и указать среди них беспорядки:

Все подстановки при :

.

Беспорядками среди них являются:

.

О том, каково количество беспорядков в общем случае, т. е. при произвольном , можно получить окончательный результат с помощью метода включения-исключения. Соответст-вующая задача называется Задачей о беспорядках.

Множество всех подстановок обозначим через , а список свойств будет состоять из свойств : свойство - это свойство той или иной подстановки оставлять на месте элемент . Ясно, что беспорядок - это как раз такая подстановка, у которой нет ни одного свойства из . Заметим, что в прежних обозначениях количество подстановок, оставляющих на месте элементы , равно ; поэтому, следуя формуле включения-исключения, получаем:

Последнее приближенное равенство основано на разложении по Тейлору функции в точке . Количество беспорядков на Символах будем обозначать символом .

Вторым примером применения формулы включения-исключения является Задача о встречах. Вот ее формулировка: имется множество подстановок на символах и задано фиксированное целое неотрицательное число ; сколько подстановок оставляют на месте

Ровно элементов? Соответствующий ответ будем обозначать символом . Очевидно, . Каждая из обсуждаемых подстановок называется Встречей (порядка ). Нетрудно установить, что

.

< Предыдущая		Следующая >