18. Линейные рекуррентные соотношения и их решение с помощью поизводящих функций. Числа Фиббоначчи

Пусть - числовая последовательность со следующим свойством:

Причем последнее равенство верно для всех , число считается фиксированным, а числа считаются изначально заданными. Таким образом, данная последовательность полностью определяется своими первыми членами ; равенство, благодаря которо-му это оказывается возможным, называется Линейным рекуррентным соотношением.

Имеется следующая классическая задача: как выразить общий член данной последо-вательности не через предыдущие члены последовательности, а в виде аналитического выра-жения от ? Приведем решение этой задачи с помощью производящий функций.

Пусть - производящая функция данной последова-тельности , которая задается линейным рекуррентным соотношением . Фиксируем следующий формальный степенной ряд: (здесь все коэффициенты, начиная с -й степени пере-менной , равны нулю). Вычислим произведение :

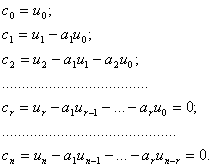
Таким образом, формальный степенной ряд - это тоже многочлен, так что производящая функция представляется как частное от деления двух многочленов:

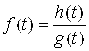Существует техника разложения таких выражений «на простейшие дроби», с помощью которой можно вычислить коэффициенты дроби в конечном виде как функции от номера коэффи-циента. Это и есть полное формальное решение рассматриваемой задачи. Рассмотрим пример.

Пусть и Такая последовательность называется Чис-лами Фиббоначчи. Последовательность чисел Фиббоначии выгляди так: 1,1,2,3,5,8,13,21... . Найдем -е число Фиббоначчи как функуцию от . Имеем: и, продолжая сохранять обозначения, ; отсюда имеет вид: