80. Граничные значения интеграла

Опр: Пусть - область и - гладкая жорданова кривая и непрерывна на по Гёльдеру с показателем . Рассмотрим интеграл .

Теорема:

Доказательство: Зададим и пусть - из леммы параграфа 79.

1 шаг: Пусть и - такие, что . Тогда

,

Где Оценим последние два интеграла. В силу выбора : 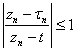, откуда получаем оценку первого интеграла: (см. лемму параграфа 79). Пусть , имеем: , откуда , пусть , тогда . Из последних оценок, получаем итог первого шага: при .

2 шаг: Пусть и . Легко видеть, что верна следующая оценка: , откуда следует, что : .

3 шаг: Оценим такую разность: 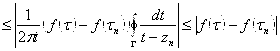. Последнее неравенство получается за счёт того, что 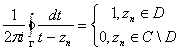, и в силу того, что : , откуда заключаем, что . Пусть теперь , тогда по неравенству треугольника: в силу всех предыдущих выкладок . Отсюда заключаем, что и в силу произвольности , откуда . Теорема доказана.

< Предыдущая		Следующая >