81. Формулы Сохоцкого-Племеля
 Пусть
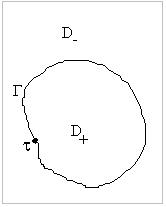
Пусть ![]() - область и
- область и ![]() - жорданова кривая и
- жорданова кривая и ![]() непрерывна на
непрерывна на ![]() по Гёльдеру с показателем
по Гёльдеру с показателем ![]() и пусть
и пусть ![]() (см. рисунок). Рассмотрим интеграл
(см. рисунок). Рассмотрим интеграл ![]() , который является аналитической функцией в
, который является аналитической функцией в ![]() и
и ![]() . И для
. И для ![]() рассмотрим пределы
рассмотрим пределы ![]() и
и ![]() . Имеем:
. Имеем: ![]() , где первый интеграл равен
, где первый интеграл равен ![]() и в силу теоремы из параграфа 81 он стремится к
и в силу теоремы из параграфа 81 он стремится к ![]() при
при ![]() . А второй интеграл:
. А второй интеграл: 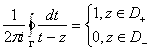 . Подставляя это, получаем две Формулы Сохоцкого-Племеля:
. Подставляя это, получаем две Формулы Сохоцкого-Племеля: ![]() и
и ![]() , и в силу того, что
, и в силу того, что ![]() и
и ![]() , получаем на границе области
, получаем на границе области ![]() Формулу скачка:
Формулу скачка: ![]() .
.
| < Предыдущая |
|---|