79. Сингулярный интеграл типа Коши
Опр: Пусть 
- область и 
- гладкая жорданова кривая и 
непрерывна на ней по Гёльдеру с показателем 
. Рассмотрим интеграл 
.
Утверждение: Этот интеграл сходится в смысле главного значения.
Доказательство: 
. Так как 
сходится абсолютно, осталось показать, что 
сходится в смысле 
Пусть 
и 
, 
, 
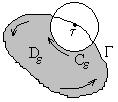
и 
(см. рисунок) 
по теореме Коши 
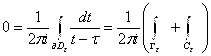, где второй интеграл берется в положительном направлении относительно 
и, следовательно, в отрицательном направлении относительно окружности 
(см. рисунок). Сделаем замену 
, 
, 
меняется против часовой стрелки (см. рисунок). Легко видеть, что при 
, разворот угла стремится к 
. После Приятных сокращений получаем: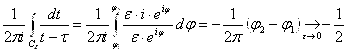 
, откуда следует, что 
. Утверждение доказано.
Следствие: Так как непрерывна по Гельдеру по условию и непрерывна по Гёльдеру по утверждению Привалова с одним и тем же показателем , то и 
будет непрерывной по Гёльдеру на 
с тем же показателем.
| < Предыдущая | Следующая > |
|---|
