73. Интегральные формулы Шварца и Пуассона

1) Пусть и - аналитическая функция в и непрерывная в , тогда верна Интегральная формула Шварца: .

Доказательство: Имеем: , . Вещественная часть функции: . Пусть , тогда в силу выкладок, получаем:

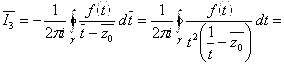
Требуемая формула получается за счёт того, что: , , . Здесь вычет в точке не учитывается, так как эта точка лежит вне круга интегрирования в силу того, что . и . Формула доказана.

2) По формуле Шварца: 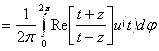. Имеем: , так как - мнимое число. Подставляя полученное выражение в последний интеграл, получаем Интегральную формулу Пуассона: .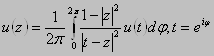

< Предыдущая		Следующая >