72. Основные свойства гармонической функции

Свойство производной: Гармоническая функция имеет производные всех порядков и эти производные являются гармоническими свойствами. Это свойство легко следует из бесконечной дифференцируемости аналитической функции.

Теорема о среднем: Для гармонической в области функции , если круг , то справедлива формула .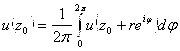

Доказательство теоремы основано на отделении действительных частей в обоих частях формулы из теоремы о среднем для аналитических функций. (см. параграф 26)

Принцип экстремума: Если гармонична в и , то если , то .

Доказательство: Пусть . Рассмотрим случай односвязной области. Тогда по следствию из теоремы параграфа 72 в существует аналитическая функция такая, что . Тогда аналитична в и не обращается в ноль. Модуль в силу монотонности функции достигает максимума в точке . Тогда . В случае многосвязной области достаточно провести аналогичные рассуждения в некотором круге достаточно маленького радиуса, чтобы . Принцип доказан.

Свойство о композиции: Если - аналитическая и - гармоническая, то гармоническая.

Доказательство: Пусть , тогда . Распишем производные: , Аналогично: , Учитывая условия Коши-Римана для функции , и гармоничность функций , получаем: . Свойство доказано.

< Предыдущая		Следующая >