66. Принцип симметрии Римана-Шварца

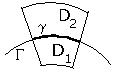Теорема: Пусть область разбивается обобщенной окружностью на , симметричные друг к другу относительно , и пусть аналитична в и , где - обобщенная окружность. Пусть - отражения соответственно плоскостей относительно . Тогда функция аналитична в .

Доказательство: Рассмотрим Частный случай - прямые и , тогда, если, то для . В . Проверим условия Коши-Римана: , так как аналитична, условия выполняются аналитична в . Тогда в силу того, то - вещественная ось и - вещественная точка и по принципу непрерывности аналитична.

Рассмотрим Общий случай. Построим ДЛО такое, чтоб и ДЛО такое, чтоб . По принципу симметрии для ДЛО симметрична к относительно , аналогично и для . На задана аналитическая функция , для которой выполнены условия частного случая и, следовательно, аналитична в , откуда получаем, что , описанная в условии теоремы, аналитична в . Теорема доказана.

< Предыдущая		Следующая >