65. Принцип непрерывности

Теорема: Пусть - область, которая разрезается гладкой жордановой дугой на две подобласти , то есть . Пусть аналитична в и аналитична в и , тогда функция является аналитической в .

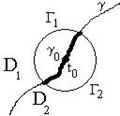
Доказательство: аналитична в и . Осталось показать, что она аналитична на . Пусть . По лемме о стандартном радиусе , , , , , , (см. рисунок). По интегральной формуле Коши для имеем: . Расписав такой же интеграл для и сложив с этим интегралом и учитывая, что получаем (интегралы по взаимоуничтожаются из-за разных направлений интегрирования): . То есть - комплексный потенциал на , который является аналитической функцией в и непрерывны на всюду в аналитична на . Для оставшейся части достаточно провести аналогичные рассуждения. Теорема доказана.

Граничная теорема единственности: Пусть аналитична в жордановой области и - гладкая жорданова дуга. Пусть , тогда в .

Доказательство: Построим область такую, что (схема построения изображена на рисунке). Пусть и . Тогда . По принципу непрерывности 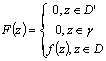аналитична в и по внутренней теореме единственности в . Теорема доказана.

Следствие: Пусть аналитичны в жордановой области и - гладкая дуга. Тогда, если , то .

Доказательство следствия проводится с помощью вспомогательной функции , которая в силу предыдущей теоремы тождественно равна нулю в области .

< Предыдущая		Следующая >