62. Лемма о раздутии
Лемма: Пусть ![]() - односвязная область такая, что
- односвязная область такая, что ![]() . Тогда существует конформное отображение
. Тогда существует конформное отображение ![]() такое, что
такое, что ![]() и
и ![]() .
.
 Доказательство: Так как
Доказательство: Так как ![]() , то
, то ![]() и в силу односвязности
и в силу односвязности ![]()
![]() - кривая, соединяющая
- кривая, соединяющая ![]() и
и ![]() такая, что
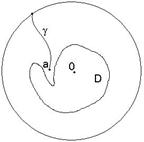
такая, что ![]() (см. рисунок). Пусть
(см. рисунок). Пусть ![]() . Тогда
. Тогда ![]() ,
, ![]() , это отображение переводит круг в себя, со смещением центра. Производная:
, это отображение переводит круг в себя, со смещением центра. Производная:  . Кривая
. Кривая ![]() соединяет
соединяет ![]() и
и ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Пусть
. Пусть ![]() - непрерывная ветвь в области
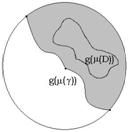
- непрерывная ветвь в области ![]() . Эта функция «разворачивает» круг в область, изображенную на втором рисунке (область, закрашенная серым цветом, лежащая в единичном круге).
. Эта функция «разворачивает» круг в область, изображенную на втором рисунке (область, закрашенная серым цветом, лежащая в единичном круге). ![]() ,
, ![]() , где рассматривается та же ветвь корня.
, где рассматривается та же ветвь корня. ![]() ,
,  . Пусть
. Пусть ![]() . Эта функция переводит единичный круг в себя, переводя точку
. Эта функция переводит единичный круг в себя, переводя точку ![]() в ноль, причем
в ноль, причем  и
и  . Тогда искомая функция есть
. Тогда искомая функция есть ![]() .
.
Действительно, ![]() ,
, ![]() ,
,  в силу того, что
в силу того, что ![]() и
и ![]()
![]()
![]() Лемма доказана.
Лемма доказана.
| < Предыдущая | Следующая > |
|---|