61. Последовательности однолистных аналитических функций (дополнение к теореме Вейерштрасса)

Пусть аналитичны в области и равномерно на компактах из , тогда по теореме Вейерштрасса аналитична в и равномерно на компактах в .

Теорема: Если вдобавок однолистны в , то либо однолистна, либо константа.

Доказательство: Пусть равномерно на компактах в и в . Допустим, что неоднолистна, то есть . Пусть , для нее - нули и кроме того - однолистны и равномерно на компактах в . Так как аналитична, то - изолированные нули - жордановая кривая, которая ограничивает область , не содержащую нулей кроме . Тогда . По теореме Вейерштрасса равномерно на компакте и на . То есть на . Рассмотрим при : . По формуле логарифмического вычета имеем: , так как не имеет в полюсов в силу аналитичности и имеет не более одного нуля в силу однолистности. 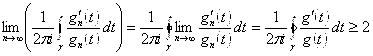. Предельный переход здесь осуществлен законно в силу равномерной сходимости на . Получили противоречие . Следовательно однолистна. Теорема доказана.

< Предыдущая		Следующая >