36. Неравенство Коши и теорема Лиувилля

Опр: аналитична в и ограничена там, т. е. , тогда при

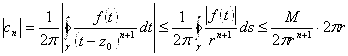, где . .

Устремив , получаем Неравенства Коши:

Теорема Лиувилля: Если аналитична на всей и ограничена, то .

Доказательство: , тогда аналитична в круге и по неравенствам Коши . Устремив , получим при . Следовательно, . И по теореме Тейлора: . Теорема доказана.

Опр: Функция, аналитическая в называется Целой. И теорема Лиувилля утверждает, что любая целая ограниченная функция есть константа.

Гипотеза Бибербаха: Пусть аналитична в , и т. е. . Каждая такая функция с указанной нормировкой будет иметь вид: Гипотеза утверждает, что если однолистна в , то имеет место оценка . Гипотеза была выдвинута в 40-х годах и доказана де Бранжем в 1986 году.

< Предыдущая		Следующая >