37. Теорема Лорана
Теорема: Пусть ![]() аналитична в кольце
аналитична в кольце ![]() , где
, где ![]() . Тогда
. Тогда ![]() имеет место разложение
имеет место разложение![]() , где
, где ![]()
![]() . Это разложение называется рядом Лорана и он сходится равномерно в
. Это разложение называется рядом Лорана и он сходится равномерно в ![]() .
.
Доказательство:
1) Покажем, что значение коэффициентов ![]() не зависят от выбора
не зависят от выбора ![]() . Рассмотрим две окружности
. Рассмотрим две окружности ![]() и
и ![]() , где
, где ![]() . Пусть
. Пусть ![]() - кольцо между окружностями
- кольцо между окружностями ![]() и
и ![]() , т. е.
, т. е. ![]() . В
. В ![]() функция
функция ![]() аналитична, т. к.
аналитична, т. к. ![]() и по теореме Коши
и по теореме Коши ![]() . А значит
. А значит ![]() , где черта во втором интеграле означает взятие интеграла в отрицательном направлении. Отсюда следует, что
, где черта во втором интеграле означает взятие интеграла в отрицательном направлении. Отсюда следует, что ![]() , а значит значения
, а значит значения ![]() не зависят от
не зависят от ![]() .
.
2) Пусть ![]() . Найдем
. Найдем ![]() такие, что
такие, что ![]() . Обозначим через
. Обозначим через ![]() окружности радиусов соответственно
окружности радиусов соответственно ![]() . Пусть
. Пусть ![]() - кольцо между этими окружностями. Функция
- кольцо между этими окружностями. Функция ![]() аналитична в нем и непрерывна вплоть до
аналитична в нем и непрерывна вплоть до ![]() . По интегральной формуле Коши имеем:
. По интегральной формуле Коши имеем: ![]() .
.
![]()
![]() - комплексный потенциал, являющийся аналитической функцией в
- комплексный потенциал, являющийся аналитической функцией в ![]() . По теореме Тейлора
. По теореме Тейлора ![]() , где
, где ![]() .
. ![]() - выражение для комплексного потенциала, следовательно:
- выражение для комплексного потенциала, следовательно: ![]()
![]()
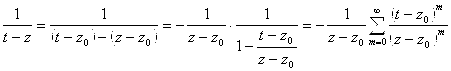 , т. к.
, т. к. 
Последний ряд есть геометрическая прогрессия, следовательно ряд сходится равномерно ![]() и его можно интегрировать.
и его можно интегрировать.


Сумма ![]() дает ряд Лорана. Теорема доказана.
дает ряд Лорана. Теорема доказана.
| < Предыдущая | Следующая > |
|---|