35. Теорема Тейлора

Теорема: Пусть аналитична в круге , тогда имеет место разложение: , где , где .

Доказательство: Пусть . Пусть и ограничивает круг, содержащий точку . По интегральной формуле Коши:

Рассмотрим тождество: . Пусть , тогда - есть сумма бесконечной геометрической прогрессии. или 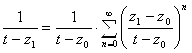- сходится равномерно по .

Подставляя это выражение в интегральную формулу Коши, получаем:

Оатслось показать независимость от выбора . В силу интегральной формулы Коши: . Слева величина не зависит от , значит, величина справа тоже не зависит от что и требовалось. Теорема доказана.

Пусть аналитична в , тогда ряд будет сходиться в , где .

< Предыдущая		Следующая >