27. Лемма о дифференцировании интеграла по аналитическому параметру

Лемма: Пусть - кусочно-гладкая дуга или кривая в , и функция задана в (т. е. ) и

непрерывна там по совокупности переменных в непрерывна в .

Тогда .- фиксировано, в является аналитической и при этом .

Опр: - метрические пространства с метриками . Тогда и .

Доказательство: Рассмотрим круг .-замкнутый круг,-компакты, значит - компакт в Непрерывна в она непрерывна на она равномерно непрерывна на . Запишем это неравенством (*):

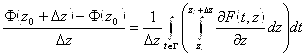Где - длина . Пусть , тогда, при , учитывая, что по формуле Ньютона-Лейбница И что и 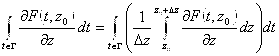, получаем следующую оценку:

. Последнее неравенство получается в силу того, что .

Лемма доказана.

< Предыдущая		Следующая >