26. Принцип максимума модуля
Теорема: Пусть ![]() аналитична в
аналитична в ![]() и
и ![]() . Если
. Если ![]() , в которой
, в которой![]() , то
, то ![]() в
в ![]() . Иными словами, модуль не постоянной функции не может достигать своей верхней границы внутри области аналитичности - только на ее границе.
. Иными словами, модуль не постоянной функции не может достигать своей верхней границы внутри области аналитичности - только на ее границе.
Доказательство: Пусть ![]() и
и ![]() . Рассмотрим множество
. Рассмотрим множество ![]() точек из
точек из ![]() , в которых
, в которых ![]() . Известно, что
. Известно, что ![]() . Покажем, что
. Покажем, что ![]() открыто. Пусть
открыто. Пусть![]() . По теореме о среднем
. По теореме о среднем ![]() достаточно малого
достаточно малого ![]() :
:
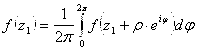 . Отсюда:
. Отсюда: 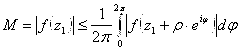 . Из условия верхней границы:
. Из условия верхней границы: ![]() на
на ![]() . Обозначим
. Обозначим ![]() на
на ![]() . Тогда имеем:
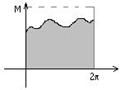
. Тогда имеем:  , но
, но  , как площади фигур (см. рисунок). Отсюда следует равенство.
, как площади фигур (см. рисунок). Отсюда следует равенство.
 , а отсюда получаем, что
, а отсюда получаем, что ![]() . Мы показали, что если
. Мы показали, что если ![]() , то
, то ![]() . Отсюда следует, что
. Отсюда следует, что ![]() открыто (любая точка лежит в нем вместе с окрестностью). Рассмотрим множество
открыто (любая точка лежит в нем вместе с окрестностью). Рассмотрим множество ![]() . Покажем, что оно открыто.
. Покажем, что оно открыто. ![]() - непрерывная вещественная функция
- непрерывная вещественная функция ![]() это неравенство выполняется в некоторой окрестности точки
это неравенство выполняется в некоторой окрестности точки ![]()
![]() - открыто. Следовательно, область
- открыто. Следовательно, область ![]() образуется двумя открытыми непересекающимися множествами, а значит
образуется двумя открытыми непересекающимися множествами, а значит ![]() является двусвязным, как область, следовательно либо
является двусвязным, как область, следовательно либо ![]() , либо
, либо ![]() . Но известно, что
. Но известно, что ![]() . Следовательно
. Следовательно ![]() является константой на всей
является константой на всей ![]() .
.
Получили: ![]() . В силу аналитичности функции (а значит, и аналитичности модуля) имеем:
. В силу аналитичности функции (а значит, и аналитичности модуля) имеем:

Заменив здесь по условиям Коши-Римана частные производные и решив относительно них систему алгебраических уравнений с ненулевыми коэффициентами, нетрудно получить, что ![]() . Следовательно
. Следовательно ![]() . Теорема доказана.
. Теорема доказана.
| < Предыдущая | Следующая > |
|---|