25. Интегральная формула Коши
Лемма: Пусть 
непрерывна в области 
и точка 
, тогда 
, где 
- окружность.
Доказательство: В силу непрерывности 
в 
: 
В силу того, что 
, оценим разность:
Отсюда следует, что 
. Это означает, что 
. Так как 
- число, следовательно, 
. 
. Лемма доказана.
Теорема: Пусть 
- область и
, 
- кусочно-гладкие жордановы кривые, а - аналитична в и непрерывна вплоть до границы 
, тогда 
верна формула:
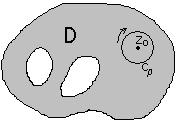Доказательство: Пусть . Построим круг 
, 
, выбрав 
достаточно малым, чтобы 
. Положим 
.
- область с кусочно-гладкой границей 
. Функция 
аналитична в , так как 
в . Следовательно, по теореме Коши: 
Здесь последний интеграл берется по часовой стрелке (область остается слева). Первый интеграл не зависит от . Во втором интеграле поменяем направление и применим лемму: 
. Теорема доказана.
25. Теорема о среднем
Теорема: Пусть аналитична в 
и непрерывна вплоть до границы. Тогда 
.
Доказательство: По интегральной формуле Коши 
. На границе круга переменная 
имеет вид 
. Отсюда получаем:
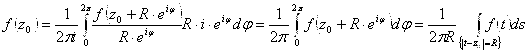
Теорема доказана.
| < Предыдущая | Следующая > |
|---|
