24. Теорема Коши для многосвязных областей

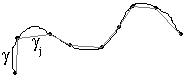Разобьем кривую на куски и построим ломаную из отрезков , как показано на рисунке. Порядок следования точек на ломаной определяется значением в них параметра, который параметризует кривую. Если при существует предел длины ломаной, то длина определяется, как этот предел, а сама кривая называется Спрямляемой. В обобщенной теореме Коши достаточна только спрямляемость границы области .

Теорема: Пусть , . Если аналитична в и непрерывна вплоть до границы, то .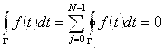

Доказательство: Докажем, используя метод математической индукции по . Для верна обобщенная теорема Коши из параграфа 23.

Пусть для некоторого теорема верна.

Докажем для .

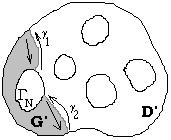
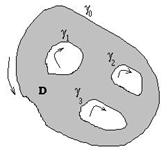
Разделим область кривыми и на две области, как показано на рисунке справа. (черта означает замыкание множества). является -связной областью и для нее в силу предположения индукции теорема верна. Отсюда получаем:

Первый интеграл равен нулю по предположению индукции, а второй в силу обобщенной теоремы Коши для односвязной области . Первое равенство имеет место в силу того, что интегралы по и при сложении взаимоуничтожаются.

Теорема доказана.

< Предыдущая		Следующая >