23. Теорема Коши
Теорема Коши: Пусть ![]() - односвязная область и
- односвязная область и ![]() - аналитичная функция. Тогда для любого кусочно-гладкого замкнутого пути
- аналитичная функция. Тогда для любого кусочно-гладкого замкнутого пути ![]() в
в ![]() (начало и конец
(начало и конец ![]() совпадают):
совпадают): ![]() .
.
Доказательство: Т. к. ![]() аналитична, то она имеет локально первообразную и обладает свойством треугольника. Т. к.
аналитична, то она имеет локально первообразную и обладает свойством треугольника. Т. к. ![]() - односвязна, то существует «глобальная» первообразная. По формуле Ньютона-Лейбница:
- односвязна, то существует «глобальная» первообразная. По формуле Ньютона-Лейбница: ![]() . Теорема доказана.
. Теорема доказана.
Лемма о стандартном радиусе: Пусть ![]() - жорданова гладкая кривая, тогда
- жорданова гладкая кривая, тогда ![]() такое, что для любого круга
такое, что для любого круга ![]() :
: ![]() - есть жорданова дуга, т. е. окружность-граница круга пересекает
- есть жорданова дуга, т. е. окружность-граница круга пересекает ![]() ровно в двух точках.
ровно в двух точках. ![]() не зависит от выбора
не зависит от выбора ![]() и называется Стандартным радиусом
и называется Стандартным радиусом ![]() .
.
Обобщенная теорема Коши: ![]() - жорданова односвязная область с гладкой (кусочно-гладкой) границей
- жорданова односвязная область с гладкой (кусочно-гладкой) границей ![]() . Если
. Если ![]() - аналитическая в
- аналитическая в ![]() и непрерывная вплоть до границы (*), то
и непрерывная вплоть до границы (*), то ![]() .
.
(*) означает, что ![]() и отсюда следует, что
и отсюда следует, что ![]() непрерывна.
непрерывна.
 Доказательство: Пусть
Доказательство: Пусть ![]() - гладкая и
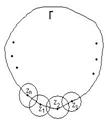
- гладкая и ![]() - ее стандартный радиус. Тогда существует конечный набор кругов
- ее стандартный радиус. Тогда существует конечный набор кругов ![]() , где
, где ![]() таких, что
таких, что ![]() и
и ![]() .
.
![]()
![]() непрерывна в
непрерывна в ![]() (компакт в
(компакт в ![]() )
) ![]()
![]() равномерно непрерывна в
равномерно непрерывна в ![]() . Зададим
. Зададим ![]() :
: ![]() . В построении потребуем, чтоб
. В построении потребуем, чтоб ![]() . Интегралы по
. Интегралы по ![]() будут вычисляться в двух направлениях и сократятся.
будут вычисляться в двух направлениях и сократятся.
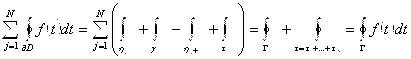 (1). Интеграл по
(1). Интеграл по ![]() равен нулю по теореме Коши.
равен нулю по теореме Коши. 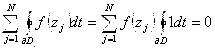 (2) по теореме Коши (константа аналитична на всей
(2) по теореме Коши (константа аналитична на всей ![]() ).
). ![]() - получается вычитанием (1)-(2).
- получается вычитанием (1)-(2). ![]() . Оценим:
. Оценим:  .
. ![]() - длина
- длина ![]() . Последняя оценка получается так:
. Последняя оценка получается так: ![]() В этой оценке первая сумма оценивает длину
В этой оценке первая сумма оценивает длину ![]() , вторая – длину
, вторая – длину ![]() . Суммы оцениваются следующим образом:
. Суммы оцениваются следующим образом: ![]() . Таким образом получаем:
. Таким образом получаем:  , откуда следует, что этот интеграл равен нулю. Теорема доказана.
, откуда следует, что этот интеграл равен нулю. Теорема доказана.
| < Предыдущая | Следующая > |
|---|