22. Лемма о треугольнике
Опр: Говорят, что функция 
, непрерывная в области 
обладает Свойством треугольника, если 
Утверждение: Если непрерывная 
в обладает свойством треугольника, то для нее локально существует первообразная.
Доказательство: 
. Пусть 
. Тогда имеем: 
. Пусть 
- треугольник с вершинами 
. Тогда: 
. Отсюда получаем далее: 
;
…
Применив 
получаем: …
…
Непрерывность: 
; … 
Отсюда следует: 
. Утверждение доказано.
Лемма о треугольнике: Если аналитическая в , то она обладает свойством треугольника (и, следовательно, имеет первообразную).
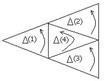Доказательство: Пусть задан треугольник 
. Обозначим: 
- периметр, 
- диаметр. Допустим, что: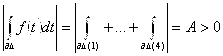 
. Тогда 
. Обозначим его через 
и применим к нему такое же разбиение. Таким образом получим последовательность 
таких, что 
. Периметр 
, диаметр 
. По лемме о вложенных компактах 
, 
, следовательно 
. В силу аналитичности функции, имеем в окрестности 
: 
. Выберем достаточно большое 
. 
. Первые два интеграла равны нулю в силу того, что для подынтегральных функций существует непрерывная первообразная, а интеграл по замкнутому контуру. Далее: 
, значит 
.Тогда 
По выбору 
: 
. Из выкладок получаем: 
или 
- противоречие, так как величина слева есть костанта. Лемма доказана.
| < Предыдущая | Следующая > |
|---|
