20. Гладкие дуги, гладкие кривые и интеграл от функции комплексного переменного
Рассмотрим непрерывную функцию ![]() .
. ![]() непрерывна по
непрерывна по ![]() .
.
Опр:![]() называется Гладким путем, если
называется Гладким путем, если ![]() и
и ![]() .
. ![]() - начало и конец пути. Если
- начало и конец пути. Если ![]() Иньективно, т. е.
Иньективно, т. е. ![]() , то дуга
, то дуга ![]() называется Гладкой дугой с началом в
называется Гладкой дугой с началом в ![]() и концом в
и концом в ![]() .
.
Опр: Жорданова дуга ![]() с концами в
с концами в ![]() и
и ![]() называется Гладкой, если существует ее гладкая параметризация, т. е. непрерывно-дифференцируемое отображение
называется Гладкой, если существует ее гладкая параметризация, т. е. непрерывно-дифференцируемое отображение ![]() , осуществляющее гомеоморфизм
, осуществляющее гомеоморфизм ![]() на
на ![]() такое, что
такое, что ![]() на
на ![]() .
.
Опр: Жорданова дуга ![]() называется Кусочно-гладкой, если существует конечный набор точек
называется Кусочно-гладкой, если существует конечный набор точек ![]() , последовательно расположенных на
, последовательно расположенных на ![]() , такой, что
, такой, что ![]() , где
, где ![]() от
от ![]() до
до ![]() - гладкая дуга.
- гладкая дуга.
Опр: Жорданова кривая ![]() называется Гладкой, если существует ее параметризация
называется Гладкой, если существует ее параметризация ![]() , где
, где ![]() - единичная окружность и
- единичная окружность и ![]() .
.
Опр: Пусть ![]() - гладкая дуга от
- гладкая дуга от ![]() к
к ![]() . Функция
. Функция ![]() задана на
задана на ![]() и непрерывна. Интегралом по дуге
и непрерывна. Интегралом по дуге ![]() от
от ![]() к
к ![]() функции
функции ![]() называется величина:
называется величина:

В формуле стоят криволинейные интегралы второго рода.
Иначе формулу можно записать так: ![]()
Свойства интеграла: 1) ![]() 2)
2) ![]() 3)
3) ![]()
4) ![]() 5)
5) 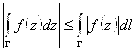 , где
, где ![]() - элемент дуги.
- элемент дуги.
Дополнительные замечания:
1) Выберем параметризацию ![]() . Тогда имеем следующее:
. Тогда имеем следующее: ![]() и
и 
2) ![]() , тогда:
, тогда:
3) Если ![]() - кусочно-гладкая, то
- кусочно-гладкая, то 
 4) Положительное направление обхода области (см. рисунок) – такой обход, при котором область остается слева.
4) Положительное направление обхода области (см. рисунок) – такой обход, при котором область остается слева.
Пусть ![]() , тогда
, тогда ![]() . Где слева стоит интеграл в положительном направлении, а справа – в отрицательном (в обозначении отрицательного направления в дальнейшем над обозначением дуги будет стоять черта).
. Где слева стоит интеграл в положительном направлении, а справа – в отрицательном (в обозначении отрицательного направления в дальнейшем над обозначением дуги будет стоять черта).
| < Предыдущая | Следующая > |
|---|