18. Комплексная логарифмическая функция

- экспоненциальная функция периодична. Рассмотрим, куда переходят область , и дуга при экспоненциальном отображении:

- луч под углом к оси .

- комплексная плоскость без неотрицательной части .

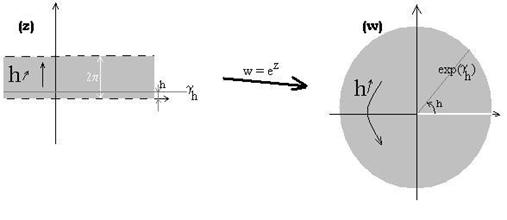
Отсюда многозначность логарифма: .

Рассмотрим :, отсюда: . Получаем формулу комплексного логарифма: .

Эта функция определена всюду при . Выделение непрерывной ветви для нее сводится к выделению непрерывной ветви аргумента.

Утверждение: Пусть-односвязная область и , тогда и , где существует единственная непрерывная ветвь функции в области такая, что , где - непрерывная ветвь аргумента в области .

Построение римановой поверхности логарифма:

Логарифм отображает риманову поверхность на комплексную плоскость (смотри рисунок).

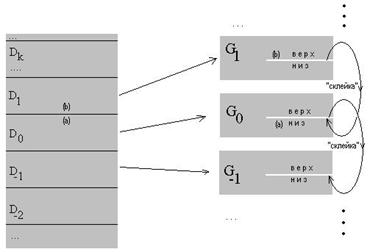
Обозначения на рисунке:

,

.

Прямые стрелки на рисунке показывают, какая область куда отображается при экспоненциальном отображении.

Риманова поверхность строится из областей путем Склеивания:

Низ разреза области то есть

Отождествляется с верхом разреза области то есть . Получается винтовая поверхность с выколотой точкой . Это и есть риманова поверхность логарифма . На ней функция логарифма является однозначной функцией. Ноль и бесконечность являются точками ветвления для римановой поверхности. Односвязная область, не содержащая точки , попадает на один лист и, соответственно, проецируется в область на . Двусвязная область, огибающая не попадает на один лист римановой поверхности и не проецируется в область на .

< Предыдущая		Следующая >