17. Выделение непрерывных ветвей многозначных функций
Опр: Пусть 
- топологические пространства. 
- множество всех непустых подмножеств 
. 
. Пусть 
и многозначное отображение: 
. Тогда непрерывное 
называется Непрерывной ветвью 
, если 
.
Задача: Пусть 
. На заданном построить непрерывную ветвь отображения , удовлетворяющую начальному условию 
.
Примеры: 1) 
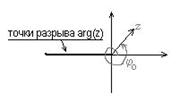
2) (рис. слева) для 
есть решение, для 
нет решения. В литературе непрерывная ветвь называется Селектором.
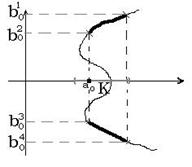
3) (рис. справа) 
задана на 
. Главное значение равно 
.
Сама функция:
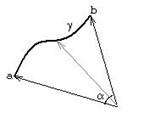
Пусть 
- жорданова дуга от 
до 
такая, что 
.
Обозначим: 
- приращение аргумента 
, когда пробегает по от к . На нижнем рисунке справа в первом случае (сверху) 
, во втором случае (снизу) 
Легко проверить, что 
и 
.
Пусть 
- односвязная область в 
и 
, тогда в 
Непрерывная ветвь 
многозначной функции : 
. Покажем корректность (рисунок слева):
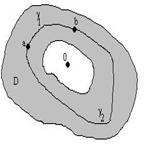
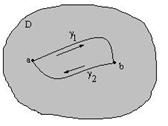
- отсюда следует корректность определения непрерывной ветви. В случае двусвязной области это уже не верно (рисунок справа).
Верна и такая формула:
.
Аналогично – приращение аргумента частного равно разности приращений аргументов.
| < Предыдущая | Следующая > |
|---|
