12. Дробно-линейные отображения (групповые свойства)

- ДЛО (дробно-линейное отображение). Последнее условие предназначено для того, чтобы выполнялось .

Обасть определения данной функции – вся комплексная плоскость, кроме точки .

Существует производная: . Она определена там же, где и сама функция и не обращается в ноль.

Существует обратное отображение: , которое строится по следующему правилу: .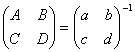

Легко показать, что композиция двух ДЛО будет также ДЛО: . Из последнего следует, что ДЛО образуют группу относительно операции композиции и эта группа изоморфна группе матриц таких что .

Рассмотрим два предела: и и доопределим функцию следующим образом: 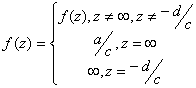. Таким образом получается непрерывная функция в . Данная функция осуществляет взаимнооднозначное отображение расширенной комплексной плоскости на себя.

При функция становится линейной : и бесконечность будет ее неподвижной точкой.

< Предыдущая		Следующая >