11. Геометрический смысл модуля и аргумента производной

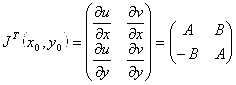; ; - это матрица Якоби для оператора производной. Якобиан равен . То есть модуль производной есть коэффициент искажения площадей на касательной плоскости при дифференцировании. Так как , значит дифференцирование сохраняет ориентацию касательной плоскости.

Рассмотрим теперь аргумент производной: .

Тогда: , то есть при дифференцировании осуществляется поворот касательной плоскости на угол величиной равной аргументу производной.

Следствия:

1) Растяжение по всем направлениям в касательной плоскости постоянно.

2) Углы между касательными кривыми сохраняется, если (консерватизм углов)

Опр: Функция , определенная в области, называется Аналитической в области , если (голоморфная).

Опр: Функция , определенная в некоторой окрестности точки , называется Аналитической в точке , если существует окрестность точки , в которой эта функция аналитична.

Опр: Отображение , где - область в , называется Однолистным (иньективным), если

Опр: Если аналитическая функция осуществляет однолистное отображение, то говорят, что Функция однолистна в области , а отображение называют Конформным.

< Предыдущая		Следующая >