10. Производная по комплексной переменной. Условия Коши-Римана

Пусть и функция определена в окрестности .

Опр: Если существует конечный , где - переменная, а выражение под знаком предела есть функция , определенная в окрестности нуля, то по определению этот предел есть Производная функции в точке : . Сама функция в данном случае называется Дифференцируемой в комплексном смысле.

Теорема Коши-Римана: Пусть определена в окрестности . Для существования производной в необходимо и достаточно:

1) и - дифференцируемы в вещественном смысле в точке

2) выполняются Условия (C-R) Коши-Римана: В точке

При этом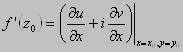

Доказательство:

Необходимость: Пусть , или . Тогда обозначим - бесконечно малая величина. ,.

Здесь - бесконечно малая величина более высокого порядка, чем .

Тогда

дифференцируемы в И существует полный дифференциал: откуда по определению полного дифференциала следует, что . Это и есть устолия (C-R). А также .

Достаточность: Пусть выполнены условия дифференцируемости функций и

и условия (C-R) .

Тогда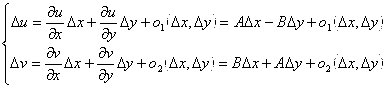

Где бесконечно малые величины и более высокого порядка, чем . Далее имеем:

Тогда так как более высокого порядка, чем .

Теорема доказана.

Примечание: Свойства производных и производные элементарных функций остаются теми же, что и для вещественной производной.

< Предыдущая		Следующая >