07. Степенные ряды. Первая теорема Абеля

Опр: Ряд вида называется Степенным рядом с центром в точке .

Числа Называются Коэффициентами ряда. Этот ряд всегда сходится при .

Первая теорема Абеля: Пусть степенной ряд Сходится в точке . Тогда:

1) Он сходится абсолютно во всех точках .

2) Он сходится равномерно на любом компакте .

Доказательство: Пункт 1 легко вывести из признака Вейерштрасса абсолютной сходимости. Докажем пункт 2.

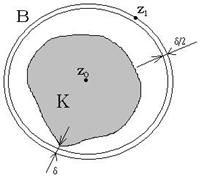Пусть ряд сходится в , тогда сходится числовой ряд . Отсюда следует, что (необходимый признак сходимости) . Определим Расстояние между множествами: .

Пусть компакт . И . Так как - компакт, то . Пусть . Тогда . Для имеем: .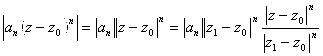

В данном разложении в силу множитель . А второй множитель 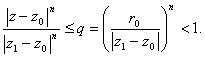Таким образом весь член ряда, начиная с некоторого оценивается . Справа стоит геометрическая прогрессия с . В силу признака Вейерштрасса ряд сходится равномерно и абсолютно на . Теорема доказана.

< Предыдущая		Следующая >