07. Оценка погрешности при замене действительного числа его подходящей дробью

Теорема 1. Для любых двух соседних подходящих дробей и к действительному числу имеет место неравенство , и если , то .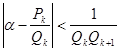

Д о к а з а т е л ь с т в о: Если , подходящие дроби и , из которых одна четная, а другая – нечетная, лежат по разные стороны от (так как точное значение непрерывной дроби находится между двумя соседними подходящими дробями), и поэтому расстояние от до любой из них меньше длины интервала, образованного этими двумя подходящими дробями, то есть

.

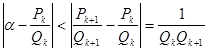Если =, то .

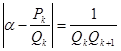Теорема 2. Для любой подходящей дроби к действительному числу справедливо неравенство:

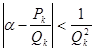
Д о к а з а т е л ь с т в о: Если =, то получаем, что левая часть неравенства равна нулю, в то время как правая часть всегда больше нуля. Поэтому при = неравенство выполняется. Пусть , то есть существует подходящая дробь .

При k>0 и согласно предыдущей теореме имеем:

.

Отдельно рассмотрим случай k=0. Если , то

.

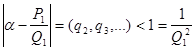Теорема 3. Если , то .

Из теорем 1-3 получаем следующие оценки погрешности:

, ,

Из которых первая является наиболее точной, а последняя – наиболее грубой.

< Предыдущая		Следующая >