11. Квадратические иррациональности и периодические цепные дроби

Рациональные числа представляют собой корни уравнений первой степени вида с целыми коэффициентами.

Во множестве иррациональных чисел наиболее простыми являются те иррациональности, которые являются корнями квадратных уравнений с целыми коэффициентами; такие числа будем называть квадратическими иррациональностями.

Число называется квадратической иррациональностью, если – иррациональный корень некоторого уравнения (1) с целыми коэффициентами, не равными одновременно нулю.

При таком , очевидно, будет a0, c0. Коэффициенты a, b, c уравнения (1), очевидно, можно взять взаимно простыми; в этом случае дискриминант этого уравнения будем называть также дискриминантом . Корни уравнения (1) равны и , так что любую квадратическую иррациональность можно представить в виде , где P, Q – целые, а D (D>1) – целое неквадратное число.

Второй корень уравнения (1) будем называть иррациональностью, сопряженной с .

В определении квадратической иррациональности особенно важно обратить внимание на то, что речь идет о квадратных уравнениях с целыми коэффициентами. Любое является корнем квадратного уравнения и даже уравнения первой степени, например уравнений , x-=0.

Примеры:

1) – квадратическая иррациональность, так как является иррациональным корнем уравнения .

2) – квадратическая иррациональность, так как представляет собой иррациональный корень уравнения . Здесь P=–1, Q=–3, D=5.

3) не является квадратической иррациональностью.

Действительно, корень любого квадратного уравнения с целыми коэффициентами имеет вид , где P, Q, D, причем D>1. Если бы мы имели =, то, возводя это равенство в куб, мы получили бы, что – рациональное число, а следовательно, рациональным являлся бы и , а это не так.

Теорема. Всякая периодическая непрерывная дробь изображает квадратическую иррациональность.

Д о к а з а т е л ь с т в о: Пусть – смешанная периодическая цепная дробь, то есть , где – чисто периодическая цепная дробь.

Обозначим подходящие дроби к и соответственно через и .

Так как , то, согласно формуле (5) из 1.1 этой главы, . Выполнив необходимые преобразования, получаем: .

Из этой формулы видно, что удовлетворяет квадратному уравнению с целыми коэффициентами. Кроме того, - число иррациональное, так как оно представляет бесконечную непрерывную дробь. Таким образом, - квадратическая иррациональность. Но по той же формуле , поэтому и является, очевидно, квадратической иррациональностью.

Докажем обратную теорему, которая носит имя Лагранжа.

Теорема Лагранжа. Всякая действительная квадратическая иррациональность изображается периодической непрерывной дробью.

Д о к а з а т е л ь с т в о: Пусть – действительный иррациональный корень квадратного уравнения (1) с целыми коэффициентами a, b, c.

При разложении в непрерывную дробь получаем (2), где – остаток порядка k+1.

Подставляя выражение из (2) в (1), получаем

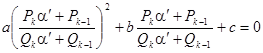
(3), где

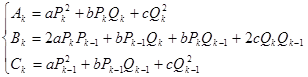(4)

Отсюда, во-первых, видно, что (5), во-вторых, можно непосредственным вычислением установить, что (6).

Таким образом, дискриминант уравнения (3) такой же, как и дискриминант уравнения (1), откуда следует, что он от k не зависит.

Идея доказательства в дальнейшем заключается в том, чтобы показать, что при данном коэффициенты , , ограничены по модулю.

Если этот факт на самом деле имел бы место, то это означало бы, что коэффициенты, будучи целыми числами, могут принимать только конечное число различных значений. Вместе с тем и число возможных уравнений (3) было бы конечным, хотя k пробегает бесконечное множество значений. Но в таком случае и остатки (которые определяются из (3)), число которых бесконечно, могли бы принять только конечное число различных значений. Поэтому должны были бы существовать остатки с одинаковыми значениями, а это уже означает, что непрерывная дробь – периодическая.

Итак, докажем, что , и ограничены по абсолютной величине. Достаточно сделать это для , так как в силу соотношения (5), из ограниченности уже как следствие вытекает ограниченность , а в силу (6) – ограниченность .

Как известно из свойств подходящих дробей, 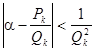или , где , откуда .

Поэтому из первого равенства (4) имеем

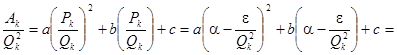
Так как , то

,

То есть 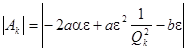и , а это и доказывает ограниченность .

Этим и завершается доказательство теоремы Лагранжа.

Отметим без доказательства следующие свойства разложений квадратических иррациональностей:

1) при разложении квадратного корня и целого положительного числа, не являющегося полным квадратом, период начинается со второго звена;

2) чисто периодическая цепная дробь получается тогда и только тогда, когда квадратическая иррациональность больше 1, а сопряженная иррациональность лежит в интервале (-1; 0) (это свойство было доказано Э. Галуа в 1828 году. Он доказал также, что в случае чисто периодического разложения сопряженная квадратическая иррациональность имеет те же элементы, но расположенные в обратном порядке).

Примеры:

1. Составить уравнение, один из корней которого разлагается в периодическую цепную дробь x и найти соответствующую иррациональность x=((2, 6, 1)).

Решение: x=(2, 6, 1, x).

Составляем схему вычисления числителей и знаменателей подходящих дробей.

	2	6	1	X
1	2	13	15	15x+13
0	1	6	7	7x+6

Итак, , откуда получаем: .

Положительное решение этого уравнения дает искомую периодическую дробь.

((2, 6, 1))= - квадратическая иррациональность. Заметим, что >1, а – иррациональность, сопряженная с x – лежит в интервале (-1; 0).

2. Составить уравнение, один из корней которого разлагается в периодическую цепную дробь x=(3, (2, 1)) и найти соответствующую иррациональность.

Решение x=(3, y), где y=(2, 1, y). Составляем схему для вычисления числителей и знаменателей подходящих дробей y:

	2	1	Y
1	2	3	3y+2
0	1	1	Y+1

Следовательно, , . Так как y>0, то мы должны взять положительный корень этого уравнения . Поэтому для x имеем . Таким образом, искомая дробь (3, (2, 1))=. Для соответствующего квадратного уравнения имеем , откуда получаем: .

< Предыдущая		Следующая >