091. Exponential Smoothing

Exponential smoothing also has the effect of smoothing out a series. It also provides an effective means of prediction. First-order exponential smoothing is used when the data do not exhibit any trend pattern. The model contains a self-correcting mechanism that adjusts forecast on the opposite direction of past errors. The equation is

Ft+1 = αAt + (1-α)Ft, (8.1)

Where Ft+1 is the forecast for the next time period

At is the actual, observed value for the current time period

Ft is the forecast previously made for the current time period

α is a “smoothing constant” which is given a value between and 1. Since the data do not trend up or down but fluctuate around some long-term average, the value Ft+1 is taken as the forecast for any future time period.

Thus, Exponential smoothing is a forecasting tool in which the forecast is based on a weighted average of current and past values.

Example. Suppose it is currently the last business day of February. Sales for Uncle Vito’s Used Cars for the month have been compiled and total $110 thousand. Uncle Vito has decided to forecast sales for March.

Table 8.3 – Uncle Vito’s Auto Sales ($1000)

Month	Forecast	Actual	Error (Ft - At)
January	-	105
February	105	110	-5.0
March	106.5	107	-0.5
April	106.65	112	-5.35

According to (8.1), the March forecast, Ft+1, requires

A. February’s actual sales, At.

B. The forecast for February, Ft.

However, since March is the first month in which Uncle Vito is developing his forecast, there was no forecast made for February and Ft is unknown. The general practice is to simply use the actual value of the previous time period, January in this case, for the first forecast.

Uncle Vito’s records show that January sales were $ 105 thousand. Assuming a value of 0.3 for α, the forecast for March is

Ft+1 = αAt + (1-α)Ft = αAFeb + (1-α)FFeb = 0.3*110 + 0.7*105 =

= $ 106.5 thousand as the forecast for sales in March.

As table 8.3 reveals, Uncle Vito can plan for sales of $ 106.5 thousand. If actual sales in March are $ 107 thousand, the error is computed as Ft - At = 106.5 – 107 = -0.5. Also, FApr = (0.3)(107) + (0.7)(106.5) = 106.65.

Assume sales in April prove to be $112 thousand. The error is then - $ 5.35 thousand. Uncle Vito can also predict sales for May:

Ft+1 = αAt + (1-α)Ft = αAApr + (1-α)FApr = 0.3*112 + 0.7*106.65 =

= $ 108.26 thousand.

The value selected for α is critical. Since it’s desirable to produce a forecast with the smallest possible error, the α – value that minimizes the Mean square error (MSE) is optimal. Trial and error often serves as the best method to determine the proper α – value. Table 8.4 contains Uncle Vito’s actual sales data for the first seven months.

Table 8.4 – Sales Data for Uncle Vito

Month	Actual	Forecast (α = 0.3)	Error	Forecast (α = 0.8)	Error
January	105
February	110	105.00	-5.0	105.00	-5.0
March	107	106.50	-0.5	109.00	2.00
April	112	106.65	-5.35	107.40	-4.60
May	117	108.26	-8.74	111.08	-5.92
June	109	110.88	1.88	115.82	6.82
July	108	110.32	2.32	110.36	2.36
August		109.62		108.47

Errors are based on forecasts calculated using α – values of 0.3 and 0.8. The MSE is

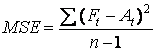. (8.2)

For α = 0.3, the MSE is

.

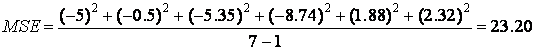An α of 0.8 yields

.

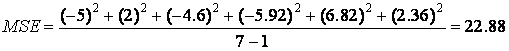An α of 0.8 produces better forecasting results since it generates a smaller error factor. Other values of α may be tried to determine their impact on MSE and the accuracy of the resulting forecasts. Generally speaking, if the data are rather volatile, a lower α-value is called for. This is because smaller values for α assign less weight to more recent observations. If the data show considerable movement, the last observation may not be representative of the long-run average.

Remember, first-order exponential smoothing in the manner described here is appropriate if the data show no trend, but move around some average value over the long run. If a downward or upward trend can be detected by plotting the data, second-order exponential smoothing, the mechanics of which will not be examined here, should be used.

Unlike moving averages, which use only a set number of time periods of data, exponential smoothing uses all past values of the time series. This is because Ft+1 depends on At and Ft. Yet, Ft used At-1 and Ft-1 in its calculation, and Ft-1 used At-2 and Ft-2. Thus, each forecast depends on previous actual values of At-n all the way back to where the forecasts first began. The farther back in time you go, the less emphasis a value of A has on the current forecast.

< Предыдущая		Следующая >