079. The Predictive Interval for a Single Value of Y

If X was set to some amount just one time, then the researcher would get one resulting value of Y. So he can be 95 (or other) percent certain that that single value of Y falls within the specific interval.

The standard error of the forecast (not standard error of the confidence mean, SY) must be calculated first. It accounts for the fact that individual values are more dispersed than are means.

, (7.6.3)

The predictive interval for a single value of Y, Yx is then

C. I. for Yx = Ŷ ± T, (7.6.4)

Example. After receiving the interval estimate for the conditional mean from the marketing division, the CEO now demands to know what the estimate is for passengers the next time they spend X = $ 10000 for advertising. the head of the marketing division realizes that what the CEO is asking for the predictive interval estimate for a single value of X.

Solution.

.

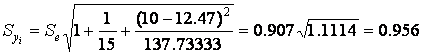Since

Ŷ = 4.4 + 1.08(10) = 15.2,

C. I. for Yx = Ŷ ± T = 15.2 ± (2.160)(0.956) = 15.2 ± 2.065,

13.14 < Yx < 17.27.

Interpretation. We can 95 percent certain that if any single month X = $ 10000, the resulting single value of Y will be between 13140 and 17270 passengers. This interval is wider that the first because researcher is working with less predictable individual values.

< Предыдущая		Следующая >