078. The Conditional Mean for Y
The Conditional Mean for Y is the population mean for all Y-values under the condition that X is equal to a specific value.
To calculate confidence interval for the conditional mean of Y, The standard error of the conditional mean Sy must be determined. It recognizes that a sample is used to calculate b0 and b1 in the regression equation. It is determined by
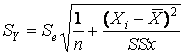 , (7.6.1)
, (7.6.1)
Where Se – the standard error of the estimate;
Xi – the given value for the independent variable.
Thus the C. I. for the conditional mean is
C. I. for µY|x = Ŷ ± TSY, (7.6.2)
Where Ŷ – the point estimator found from the original regression equation ;
T-value is based on a selected level of confidence with N-2 degrees of freedom. There are N-2 d. f. because two values b0 and b1 must be calculated from the sample data. Therefore two d. f. are lost.
The C. I. for µY|x could be calculated at several X-values. Thus, several C. I. would then form an entire confidence band for µY|x. The band becomes wider at the extremes. This happens because regression analysis is based on averages, and the father researcher is away from the center point, the less accurate his results (Fig.7.11).
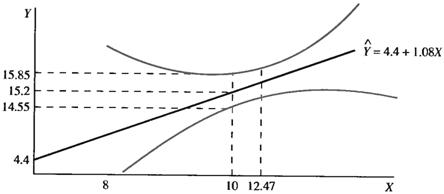
Figure 7.11 – Confidence limits for µY|x for Hop Scotch from Table 7.2
| < Предыдущая | Следующая > |
|---|