075. Correlation Analysis. Coefficient of Determination

The job of correlation analysis is to measure the strength of the relationship between Y and X in the regression model. This measure of strength is provided by the coefficient of determination R. The Coefficient of determination is one of the measures of goodness-of fit along with the standard error of the estimate Se.

To understand correlation analysis, the Total deviation of Y (Yi - ) has to be considered. The Total deviation is the amount by which an actual value of Y, Yi, differs from , the mean of all the values for the dependent variable.

The total deviation can be broken down into types. The Explained deviation and Unexplained deviation. The Explained deviation is that portion of the total deviation that is explained by the regression model, is the difference between the value predicted by the model and the mean value of Y: (Ŷ - ). The Unexplained deviation is the difference between the actual value Yi and that value predicted by the model: (Yi - Ŷ).

As an example the data from Table 7.2 are considered. Taking month 13, it’s shown that 23000 people flew on Hop Scotch (Yi = 23). Since the mean value for the number of passengers is

.

The total deviation for the thirteenth month is 23-17.87=5.13.

On the other hand, the regression model forecasts a value for Y of

Ŷ = 4.4 + 1.08*(16) = 21.68.

Using the regression model the error is only Yi - Ŷ =23-21.68 = 1.32. This value is much closer to the actual value for passengers than the average value for Y as a prediction.

This is shown in Figure 7.9.

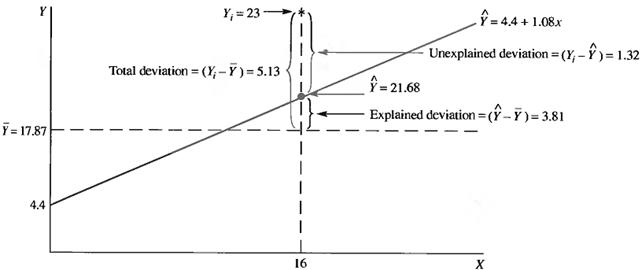
Figure 7.9 – Deviations for Hop Scotch Airlines

Then

Total deviation = Explained deviation + Unexplained deviation

That is,

(Yi - ) = (Ŷ - ) + (Yi - Ŷ).

To prevent negative errors from offsetting the positive errors, the squaring process is necessary. Thus, the total sum of squares (SST), the regression sum of squares (SSR) and the error sum of squares (SSE) respectively are

SST = Σ(Yi - )2; SSR = Σ(Ŷ - )2; SSE = Σ(Yi - Ŷ)2.

The Coefficient of determination R2,

- it is a ratio of the explained deviation to the total deviation,

- it is a measure of the explanatory power of the regression model by measuring what portion of the change in Y is explained by the change in X,

- measures the strength of the Linear relationship between X and Y.

R2 = .

In terms of sums of squares and cross products it can be calculated as

.

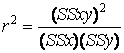The Value for r2 must be between 0 and 1 since more that 100 percent of the change in Y cannot be explained. The higher the R2, the more explanatory power the model has. If R2 = 70 percent, this means 70 percent of the variation in Y is explained by changes in X.

Example. Given the data for Hop Scotch from Table 7.2, the coefficient of determination is

.

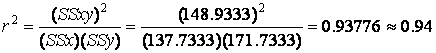Interpretation. The coefficient of determination reveals that 94 percent of the change in the number of passengers is explained (not caused) by changes in advertising expenditures.

Since = 0.94, the model explains 94 percent of the change in Y. the other 6 percent can be explained by some variable(s) other than advertising. This 6 percent sometimes referred to as the Coefficient of nondetermination, .

< Предыдущая		Следующая >