074. The Standard Error of the Estimate: A Measure of Goodness-of-Fit
The formula to calculate the standard error of the estimate is the following
 , or
, or ![]() , where
, where ![]() - the mean square error;
- the mean square error;
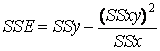 - the error sum of squares;
- the error sum of squares;
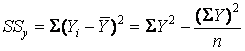 - the sum of squares of Y.
- the sum of squares of Y.
The Standard error of the estimate, Se, is quite similar to the standard deviation of a single variable, and is a measure of the average amount by which the actual observations for Y vary around the regression line. It gauges the variation of the data points above and below the regression line. As a measure of the dispersion of the Y-values around the regression line, it reflects a tendency to depart from the actual value of Y when using the regression model for prediction purposes. In that sense, it is a measure of the average amount of the error.

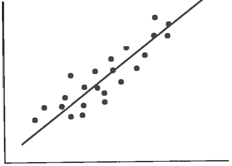
A B
Figure 7.7 – Possible Scatter Diagrams: A – Se = 0; B – Se ≠ 0
The more dispersed the original data are, the larger Se will be (Fig.7.8).
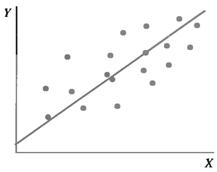
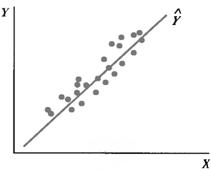
A B
Figure 7.8 – A Comparison of the Standard Error of the Estimate
As indicated by the scatter diagrams in Figure 7.8, the data for Fig.7.8(a) are much more dispersed than those on Fig.7.8(b). The Se for Fig.7.8(a) would therefore be larger.
| < Предыдущая | Следующая > |
|---|