38.3. Основные теоремы операционного исчисления

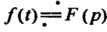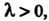Теорема 38.3. (Теорема подобия). ЕслиИТо умноже

Ние аргумента оригинала на положительное число приводит к делению изображения и его аргумента на это число:

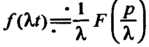(38.16)

Теорема 38.4. (Теорема смещения). ЕслиИ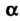- произвольное

Комплексное число, то изменение (смещение) аргумента изображения на величину а приводит к умножению оригинала на величину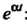

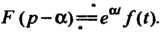(38.17)

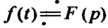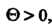Теорема 38.5. (Теорема запаздывания). ЕслиИТо за

Паздывание аргумента оригинала на положительное число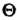Приводит к умножению изображения на величину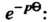

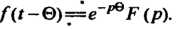(38.18)

Теорема 38.6. (Теоремаумножения). Если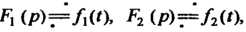То

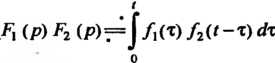(38.19)

Замечание. Интеграл в правой части этой формулы называется складкой, или сверткой функци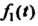иИ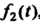, а операция получения складки называется свертыванием функций. В связи с этим теорему умножения можно сформулировать так: умножение изображений приводит к свертыванию их оригиналов. Эту теорему называют также теоремой свертывания и теоремой Бореля.

Свертка функций обладает переместительным свойством:

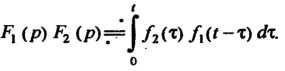
Поскольку функцияравна нулю при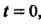То, поль

Зуясь правилом дифференцирования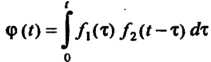Оригинала, получаем следующую запись теоремы умножения:

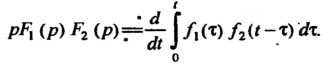(38.20)

Интеграл в правой части этой формулы называется интегралом Дюамеля. Если выполнить дифференцирование в интеграле Дюамеля, то теорема умножения примет ввд

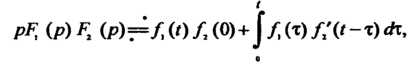
Или, учитывая равноправность функций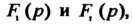

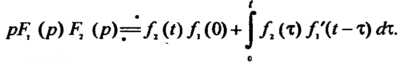
Примененное здесь правило дифференцирования интеграла по переменной, входящей в качестве параметра в подынтегральную функцию и в верхний предел интегрирования, определяется формулой

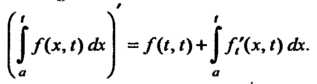(38.21)

Последние две записи теоремы умножения можно видоизменить, если учесть, что

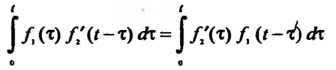
И

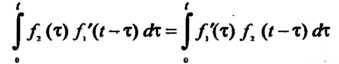
Теорема 38.7. Если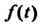— оригинал с периодом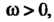То его изображе

Ние выражается формулой

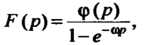(38.22)

Где

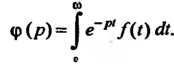(38.23)

Эту теорему называют теоремой об изображении периодического оригинала Теорема 38.8. Если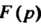—аналитическая функция в окрестности беско

Нечно удаленной точки и равна в ней нулю и если лорановское разложениеВ

Окрестности бесконечно удаленной точки имеет вид

То оригиналом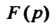Служит функция

Причем этот ряд сходится при всех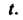

Эту теорему называют первой, теоремой разложения.

Пример 38.14. Найти изображение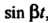, зная изображение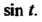

Поскольку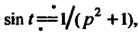То в соответствии с теоремой подобия

(см. (38.16)) получаем

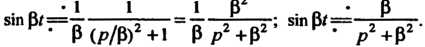
Пример 38.15. Найти изображение функций: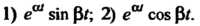

Пользуясь формулами

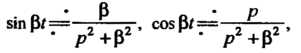
С помощью теоремы смещения находим

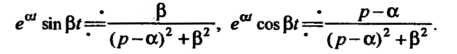
Пример 38.16. Найти изображение функции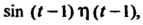Где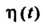

- функция Хевисайда (см. 38.1).

Вцд функции показывает, что здесь имеется запаздывание аргумента на величину 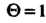. С помощью теоремы запаздывания и формулы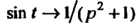Получаем

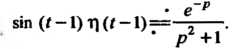
Замечание. Если бы запаздывания аргумента не было, т. е. рассматривалась функция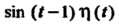(такую функцию условились обозначать просто 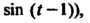То изображение имело бы совсем другой вид, а именно:

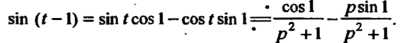
Пример 38.17. Найти изображение функции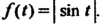 Поскольку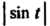— периодическая функция с периодом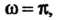То изображе

Ние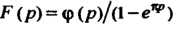(см. формулу (38.22)), где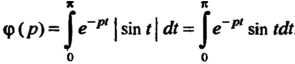

Дважды проинтегрировав по частям, получим 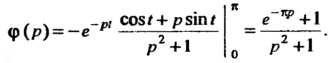 Следовательно,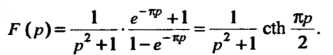

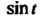Пример 38.18. Найти изображение периодического оригиналаС периодом, который равенПри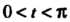И нулю при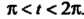

Оригинал для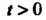Можно записать так: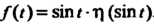. Искомое изобра

Жение имеет вид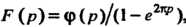Где

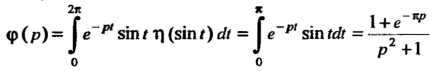
(см. пример 38.17). Итак,

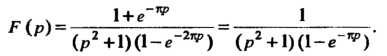
Пример 38.19. Найти оригинал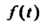По его изображению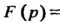

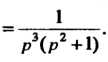Г

Изображению придадим другой вид: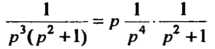И будем счи

Тать, что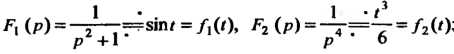; здесь использо

Вано равенство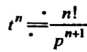• при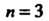(см. пример 38.8). С помощью теоремы ум

Ножения (см. формулу (38.20)) получаем

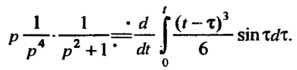
В соответствии с формулой (38.21) находим производную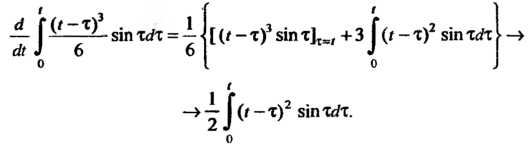

Дважды интегрируя по частям, получаем

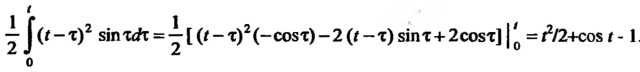
Следовательно,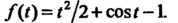

П р й м е р 38.20. Найти оригинал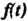Для изображения 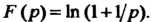Использовав разложение функцииВ ряд Тейлора (см. п. 37.6)

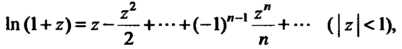
Получим

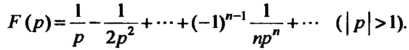
В соответствии с теоремой (38.8) находим оригинал

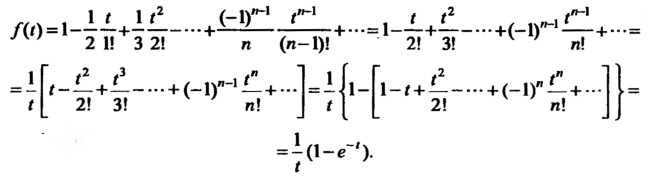
< Предыдущая		Следующая >