38.2. Основные правила и формулы операционного исчисления

Свойство линейности. Если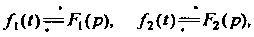А

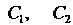
Произвольные постоянные, то

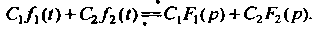(38.6)

В частности, изображение суммы функций определяется формулой

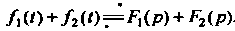
Дифференцирование оригинала. Если функции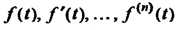Явля

Ются функциями-оригиналами и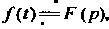То

Где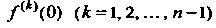Есть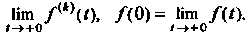

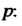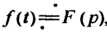Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения наЕсли, то

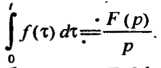(38.9)

Дифференцирование изображения. Дифференцирование изображения сводится к умножению оригинала на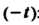: если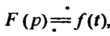, то

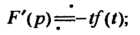(38.10)

В общем случае

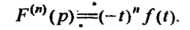(38.11)

Интегрирование изображения. Если интегралсходится, то он яв

Ляется изображением функции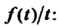

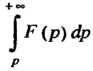
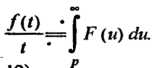(38.12)

С помощью формулы (38.м.) можно вычислять некоторые несобственные интегралы. Если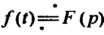И интеграл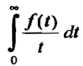Сходится, то

(38.13)

Где интеграл в правой части вычисляется по положительной полуоси.

Предельные соотношения. Если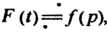То

(38.14)

Где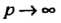Вдоль положительного направления вещественной оси.

Если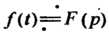И существует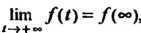, то

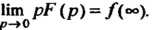(38.15)

Пример 38.4. Найти изображения тригонометрических функций: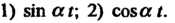

На основании формулы (38.5) получаем 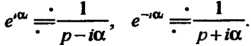 В соответствии с формулой (38.6) при

4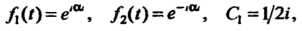

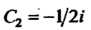Находим:

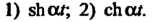
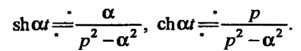
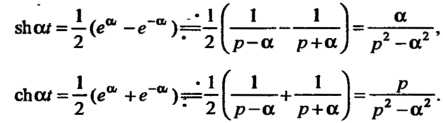
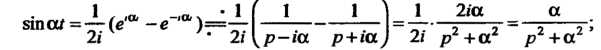
При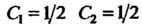Получим

Таким образом,

Пример 38.5. Найти изображения гиперболических функций: Принимая во внимание формулы (38.5) и (38.6), находим:

Следовательно,

Пример 38.6. Найти изображение функции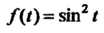С помощью

Дифференцирования оригинала.

Используем первую из формул (38.7):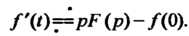Поскольку

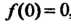, то формула принимает вид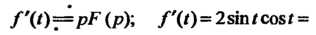

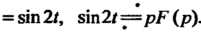Как известно (см. пример 38.4),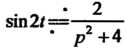, поэто

Му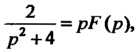Откуда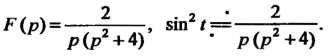

В соответствии с формулой (38.5), при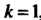, получим. На основа

Нии формулы (38.9) найдем, что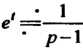

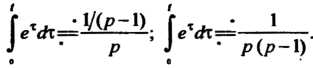
Пример 38.8. Найти изображение функции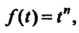Где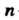

Натуральное число.

Из равенства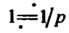(см. замечание к примеру 38.2), пользуясь правилом ин

Тегрирования оригинала, находим:

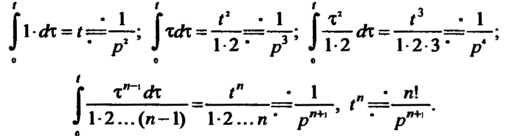
Пример 38.9. Найти изображения функций: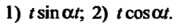

Поскольку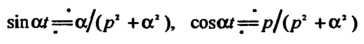(см. пример 38.4), то с

Помощью правила дифференцирования изображения (см формулу (38.10)) получим:

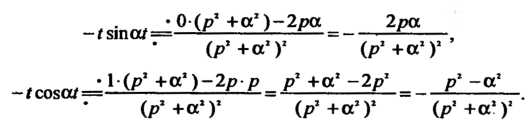
Таким образом,

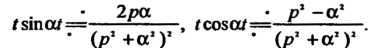
Пример 38.10. Найти изображение функции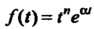, где-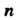

Натуральное число.

Из формулы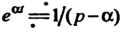(см. равенство (38.5)) n-кратным дифференциро

Ванием изображения (см. формулу (38.11)) получаем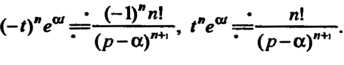

На основании равенства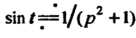(см. пример 38.4) и правила интег

Рирования изображения (см. формулу (38.12)) находим

(Для многозначных функций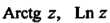И т. д. рассматривают ветви, для кото

Рых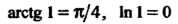И т. д).

Пример 38.12. Вычислить интеграл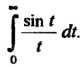

Принимая во внимание равенство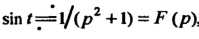, с помощью фор

Мулы (38.13) получаем

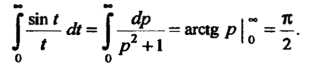
Пример 38.13. Проверить, выполняются ли предельные соотношения для следующих функций: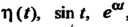, где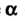- вещественное число.

Равенство (38.14) выполняется для всех этих функций. Действительно, по-

Скольку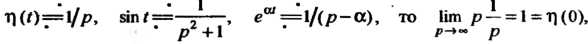

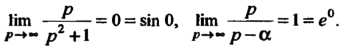
Равенство (38.15) для функции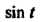Не выполняется, так какНе суще

Ствует; для функци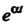иПри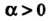Оно также не выполняется по той же причине.

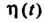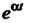Для функцийИПри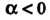Это равенство будет справедливым;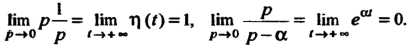

< Предыдущая		Следующая >