38.1. Оригинал и изображение
Функцией-оригиналом называется любая комплекснозначная функция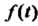 вещественной переменной
вещественной переменной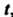 J удовлетворяющая следующим условиям:
J удовлетворяющая следующим условиям:
1.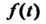 Интегрируема на любом конечном промежутке оси
Интегрируема на любом конечном промежутке оси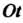 (локально интегрируема).
(локально интегрируема).
2.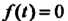 Для всех
Для всех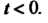
3.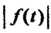 Возрастает не быстрее показательной функции, т. е. существуют такие постоянные
Возрастает не быстрее показательной функции, т. е. существуют такие постоянные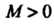 И
И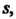 Что для всех
Что для всех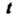
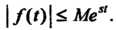
Нижняя грань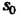 Всех чисел
Всех чисел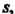 . для которых выполняется это неравенство, называется показателем роста функции
. для которых выполняется это неравенство, называется показателем роста функции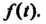
Простейшей функцией-оригиналом является единичная функция Хевисайда
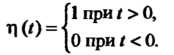 (38.1)
(38.1)
Очевидно, что
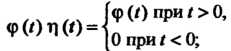
Если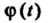 Удовлетворяет условиям 1 и 3, то
Удовлетворяет условиям 1 и 3, то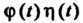 Является функцией-оригиналом.
Является функцией-оригиналом.
Для сокращения записи вместо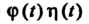 Пишут
Пишут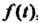 , считая, что
, считая, что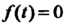 При
При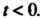
Изображением функции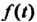 Называется функция
Называется функция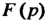 Комплексной пере
Комплексной пере
Менной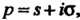 Определяемая формулой
Определяемая формулой
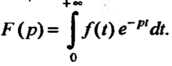 (38.2)
(38.2)
Интеграл в правой части равенства называют интегралом Лапласа, а переход от оригинала к его изображению - преобразованием Лапласа.
Тот факт, что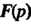 Является изображением
Является изображением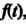 Символически записывают так:
Символически записывают так: 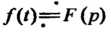
И называют операционным (или операторным) равенством. Употребляют и другие обозначения, например: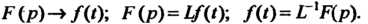
Теорема 38.1. Фунщия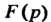 Определена в полуплоскости
Определена в полуплоскости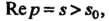 Где
Где
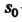 - показатель роста
- показатель роста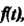 И является в этой полуплоскости аналитической функцией. Следствие. Изображение
И является в этой полуплоскости аналитической функцией. Следствие. Изображение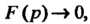 Если
Если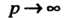 Так, что
Так, что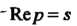
Неограниченно возрастает, а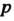 Находится в полуплоскости
Находится в полуплоскости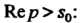
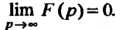
Теорема 38.2. Преобразование Лапласа
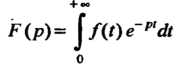
Единственно в том смысле, что две функции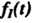 И
И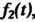 , имеющие одинаковые преобразования Лапласа, совпадают во всех точках непрерывности для всех
, имеющие одинаковые преобразования Лапласа, совпадают во всех точках непрерывности для всех Пример 38.1. Показать, что функция
Пример 38.1. Показать, что функция
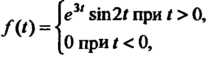
Является функцией-оригиналом.
Убедимся в том, что все три условия, определяющие функцию-оригинал, выполняются для данной функции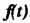 . Действительно, функция
. Действительно, функция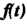 Локально интегрируема: интеграл
Локально интегрируема: интеграл
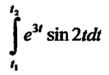
Существует для любых конечных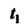 И
И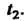 Условие 2 выполняется в соответствии с определением функции
Условие 2 выполняется в соответствии с определением функции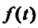 (
(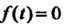 При
При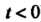 ). Наконец,
). Наконец,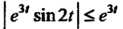 Для лю
Для лю
Бых вещественных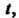 Так что в качестве
Так что в качестве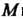 В условии 3 можно взять число
В условии 3 можно взять число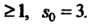
Пример 38.2. Найти изображение единичной функции Хевисайда, определяемой формулой (38.1).
В соответствии с формулой (38.2) получаем
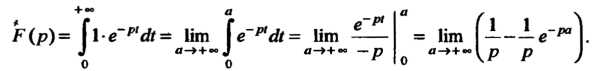
Если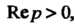 То
То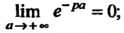 В этом случае
В этом случае
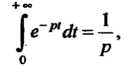 (38.3)
(38.3)
 (38.4)
(38.4)
Замечание. Изображение (38.4) получено при условии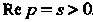 . При
. При
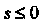 Интеграл Лапласа не существует. Однако функция
Интеграл Лапласа не существует. Однако функция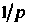 Аналитическая на всей плоскости комплексной переменной
Аналитическая на всей плоскости комплексной переменной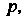 Кроме
Кроме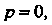 И ее значение для
И ее значение для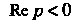
Можно рассматривать как значения изображения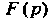 При
При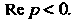 Для функции
Для функции
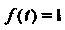 Равенство
Равенство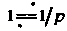 Будет выполнятся для всех
Будет выполнятся для всех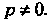
Пример 38.3. Найти изображение функции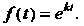 Принимая во внимание равенство (38.3), получаем
Принимая во внимание равенство (38.3), получаем
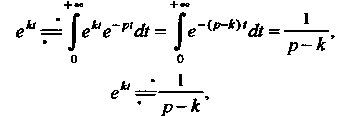 (38.5)
(38.5)
Когда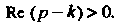 Поскольку функция
Поскольку функция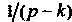 Аналитическая при всех
Аналитическая при всех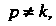
То ее можно рассматривать как изображение функции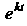 Для таких
Для таких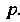
| < Предыдущая | Следующая > |
|---|