37.8. Вычеты функций

Вычетом однозначной аналитической функции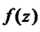В изолированной особой точке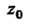Называется число, которое обозначают через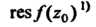И

Определяют формулой

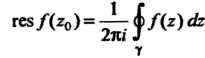(37.52)

Где интеграл - взят в положительном направлении по контуру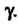(Используются и другие обозначения: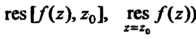L В качестве контура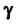Рассматрива

Ется окружность с центром в точке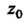Достаточно малого радиуса; такого, чтобы окружность не выходила за пределы области аналитичности функции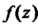И не содержала внутри других особых точек этой функции. Вычет функции равен коэффициенту при минус первой степени лорановском разложении функции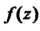В окрестности точки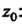

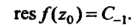(37.53)

Вычет функции в устранимой особой точке равен нулю.

Если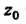- полюс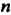-го порядка функции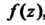, то

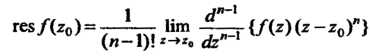(37.54)

В случае простого полюса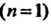

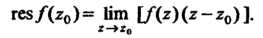(37.55)

Если функция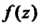В окрестности точки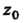Является частным двух аналитических функций

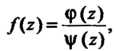
Причем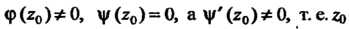- простой полюс функции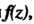То

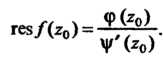(37.56)

Если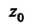Является существенно особой точкой функции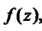То для

Нахождения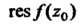Необходимо найти коэффициент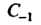В лорановском

Разложении функции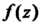В окрестности точки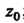; это и будет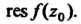

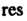!)— сокращение французского слова rlsidu, что означает вычет.

Теорема 37.2. Если функция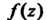Является аналитической на границе 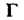области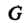И всюду внутри области, за исключением конечного числа особых точек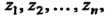То

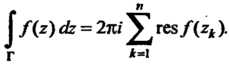(37.57)

Этой теоремой (ее называют теоремой Коши о вычетах) пользуются при вычислении определенных интегралов и нахождении сумм рядов.

Вычет функции относительно бесконечно удаленной точки. Говорят, что функция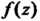Является аналитической в бесконечно удаленной точке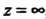, если функция

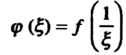
Анапитична в точке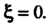Например, функция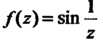Аналитична в точке

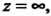Поскольку функция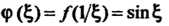Аналитична в точке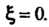

Пусть функция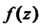Аналитична в некоторой окрестности бесконечно удаленной точки (кроме самой точки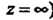I.

Говорят, что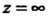Является устранимой особой точкой, полюсом или сущест

Венно особой точкой функции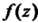Г в зависимости от того, конечен, бесконечен или вовсе не существует предел этой функции при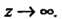

Критерии типа бесконечно удаленной особой точки, связанные с рядом Лорана, изменяются в сравнении с критериями для конечных особых точек.

Теорема 37.3. Если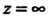Является устранимой особой точкой функции

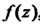, то ее лорановское разложение в окрестности данной точки не содержит положительных степеней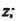Когда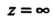— полюс, то это разложение содержит

Конечное число положительных степеней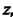В случае существенно особой точки - бесконечное множество положительных степеней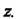

При этом лорановским разложением функции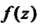В окрестности бесконечно удаленной точки называют разложение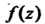В ряд Лорана, сходящийся всюду вне круга достаточно большого радиуса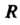С центром в точке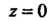(кроме, быть мо

Жет, самой точки).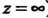

Рассмотрим функцию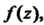Аналитическую в некоторой окрестности точки

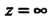(кроме, быть может, самой этой точки).

Вычетом функции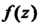В бесконечности называется величина

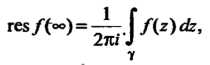(37.58)

Где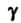- окружность достаточно большого радиуса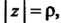Которую точка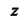

Проходит по часовой стрелке (при этом окрестность точки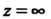Остается слева,

Как и в случае конечной точки|.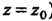

Из этого определения следует, что вычет функции в бесконечности равен коэффициенту при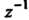В лорановском разложении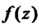В окрестности точки 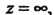взятому со знаком минус:

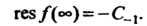(37.59)

Известные разложения функций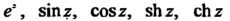(см. п. 37.2) мож

Но рассматривать как лорановские ряды в окрестности точки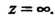Поскольку

Каждый ряд содержит бесконечное множество положительных степеней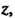То указанные функции имеют в точке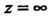Существенную особенность.

Теорема 37.4. Если функция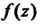Имеет в расширенной комплексной плоскости конечное число особых точек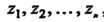, то сумма всех ее вычетов, включая и вычет в бесконечности, равна нулю:

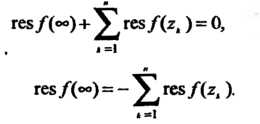(37.60)

Последнее равенство используется при вычислении некоторых интегралов.

Пример 37.38. Найти вычет функции-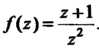

Данную функцию можно записать так: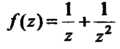И рассматривать эту сумму

Как разложение в ряд Лорана по степеням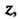Для которого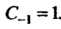В соответствии с

Формулой (37.53) находим, что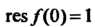(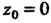- особая точка).

Замечание. Вычет можно найти и с помощью формулы (37.54). Поскольку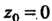- полюс второго порядка, то

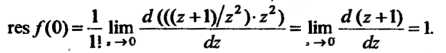
Пример 37.39. Найти вычеты функции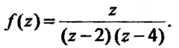

Эта функция имеет два простых полюса: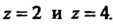В соответствии с фор

Мулой (37.55) находим: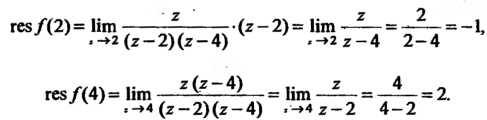

Поскольку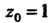- полюс третьего порядка, то на основании формулы (37.54)

Получаем

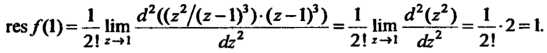
Пример 37.41. Найти вычет функции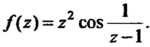

Точка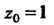Является единственной конечной особой точкой функции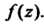

Чтобы найти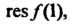Разложим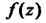В ряд Лорана в окрестности точки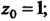

При этом используем ряд Тейлора для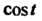(см. (37.5))

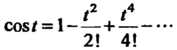
При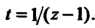Это разложение принимает вид

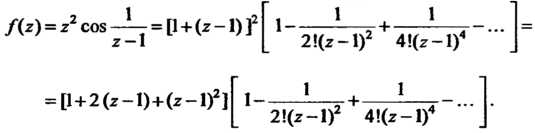
Нас интересует только коэффициент при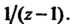Соответствующий член ряда

Имеет вид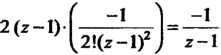. Значит,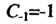, поэтому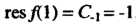

Пример 37.42. Вычислить интеграл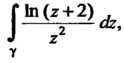Где- окружность

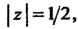Которую точка z проходит в положительном направлении.

В круге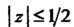Содержится только одна особая точка подынтегральной

Функции - это полюс второго порядка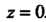. Вычет функцииВ точке найдем в соответствии с формулой (37.54):

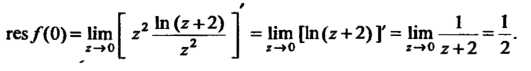
На основании формулы (37.52) получаем: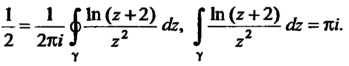

Ях: 1)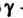- окружность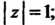2)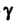- окружность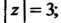3)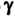- окружность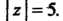

В соответствии с формулой (37.55) найдем сначала вычеты функции 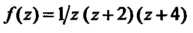Относительно простых полюсов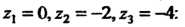

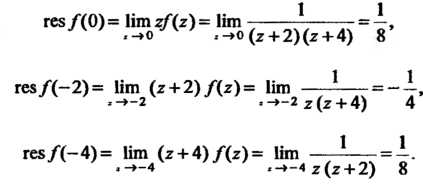
Интегралы найдем с помощью формулы (37.57).

В первом случае в области, ограниченной окружностью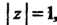, находится

Только один полюс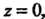Поэтому

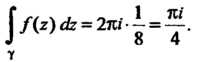
Во втором случае окружность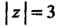Ограничивает область, которая содержит

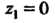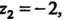ПолюсыИ.Тогда

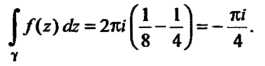
В третьем случае внутри области, ограниченной контуром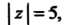Находятся

Три полюса: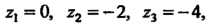Поэтому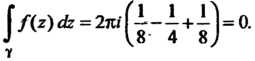

Гпава 38

ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ

< Предыдущая		Следующая >