37.7. Нули функции. Особые точки
Нули функции. Рассмотрим функцию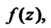 Аналитическую в точке
Аналитическую в точке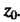 Точка
Точка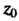 называется нулем функции
называется нулем функции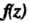 Порядка (или кратности)
Порядка (или кратности)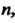 Когда выполняются условия:
Когда выполняются условия:
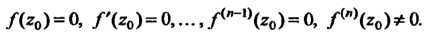 (37.47)
(37.47)
Если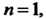 То точка
То точка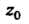 Называется простым нулем.
Называется простым нулем.
Значение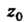 Тогда и только тогда является нулем и-го порядка функции f(z), аналитической в точке
Тогда и только тогда является нулем и-го порядка функции f(z), аналитической в точке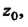 Когда в некоторой ее окрестности верно равенство
Когда в некоторой ее окрестности верно равенство
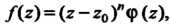 (37.48)
(37.48)
Где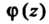 - функция, аналитическая в точке
- функция, аналитическая в точке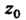 И
И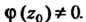
Особые точки. Особой точкой функции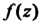 Называется точка
Называется точка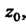 В которой эта функция не является аналитической. Точка
В которой эта функция не является аналитической. Точка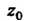 Называется изолированной особой точкой функции
Называется изолированной особой точкой функции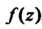 , когда существует окрестность этой точки, в которой
, когда существует окрестность этой точки, в которой 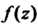 Аналитическая всюду, кроме
Аналитическая всюду, кроме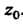 . Особая точка
. Особая точка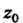 Функции
Функции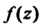 Называется устранимой, когда существует конечный предел этой функции в данной точке:
Называется устранимой, когда существует конечный предел этой функции в данной точке: 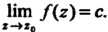 Точка
Точка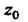 Называется полюсом функции
Называется полюсом функции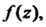 Когда
Когда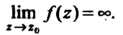
Для того, чтобы точка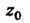 Была полюсом функции
Была полюсом функции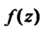 Необходимо и достаточно, чтобы эта точка была нулем. функции
Необходимо и достаточно, чтобы эта точка была нулем. функции
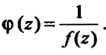 (37.49)
(37.49)
Точку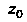 Называют полюсом порядка
Называют полюсом порядка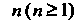 Функции
Функции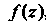 , когда эта
, когда эта
Точка является нулем порядка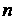 Для функции
Для функции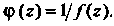 В случае
В случае
Полюс называют простым.
Для того, чтобы точка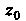 Являлась полюсом порядка
Являлась полюсом порядка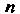 Функции
Функции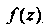 , необходимо и достаточно, чтобы функцию
, необходимо и достаточно, чтобы функцию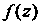 Можно было привести к виду
Можно было привести к виду
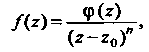 (37.50)
(37.50)
Где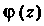 - функция, аналитическая в точке
- функция, аналитическая в точке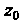 И
И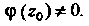
Точка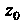 Называется существенно особой точкой функции
Называется существенно особой точкой функции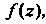 Когда в ней
Когда в ней
Функция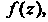 Не имеет ни конечного ни бесконечного предела.
Не имеет ни конечного ни бесконечного предела.
Справедливы следующие утверждения.
1. Точка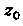 Является устранимой особой точкой функции
Является устранимой особой точкой функции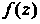 Тогда и только тогда, когда ее лорановское разложение в окрестности точки
Тогда и только тогда, когда ее лорановское разложение в окрестности точки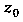 Не содержит главной части.
Не содержит главной части.
2. Точка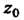 Является полюсом функции
Является полюсом функции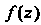 Тогда и только тогда, когда главная часть ее лорановского разложения в окрестности точки
Тогда и только тогда, когда главная часть ее лорановского разложения в окрестности точки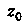 Содержит только конечное число членов:
Содержит только конечное число членов:
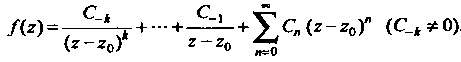 (37.51)
(37.51)
Наибольший из показателей степени разности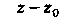 В знаменателях
В знаменателях
Совпадает с порядком полюса.
3. Точка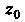 Является существенно особой точкой функции
Является существенно особой точкой функции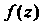 Тогда и только тогда, когда главная часть ее лорановского разложения в окрестности точки
Тогда и только тогда, когда главная часть ее лорановского разложения в окрестности точки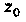 Содержит бесконечное множество членов.
Содержит бесконечное множество членов.
Пример 37.31. Доказать, что точка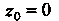 Является нулем второго по
Является нулем второго по
Рядка для функции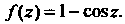
Разложим в ряды данную функцию и ее первую и вторую производные: 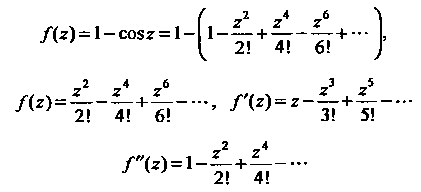
Поскольку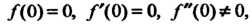 Т. е. выполняются условия (37.47)
Т. е. выполняются условия (37.47)
При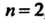 , то
, то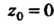 — нуль второго порядка для функции
— нуль второго порядка для функции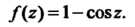
Пример 37.32. Найти порядок нуля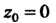 Для функции
Для функции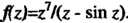
Использовав разложение функции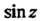 В ряд Тейлора, получим
В ряд Тейлора, получим
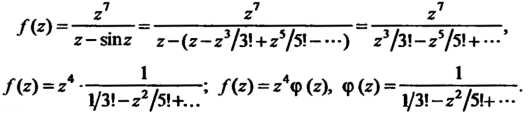
Таким образом, функция _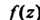 . j записана в виде (37.48), где
. j записана в виде (37.48), где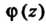 - функция, аналитическая в точке
- функция, аналитическая в точке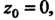 Причем
Причем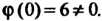 Значит, точка
Значит, точка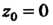 - нуль
- нуль
Четвертого порядка для данной функции.
Пример 37.33. Найти нули функции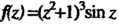 И определить их порядки.
И определить их порядки.
Когда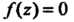 Или
Или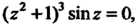 То
То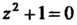 Либо
Либо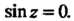 Из первого
Из первого
Равенства следует, что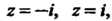 А со второго, что
А со второго, что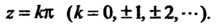
Пусть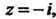 Тогда функцию
Тогда функцию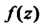 Можно представить в виде (37.48):
Можно представить в виде (37.48):
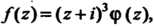 Где функция
Где функция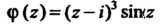 Является аналитической в
Является аналитической в
Точке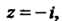 Причем
Причем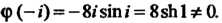 Значит, точка
Значит, точка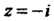 Есть нуль
Есть нуль
Третьего порядка. Аналогично доказывается, что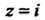 —нуль третьего порядка. Функция
—нуль третьего порядка. Функция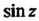 Имеет нули
Имеет нули
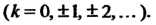 Действительно,
Действительно,
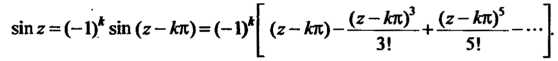
Это нули первого порядка для функции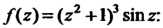
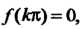 Но
Но
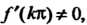 Ибо
Ибо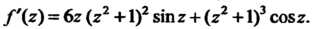
Пример 37.34. Доказать, что точка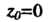 Для функции
Для функции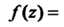
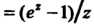 Является устранимой особой точкой.
Является устранимой особой точкой.
Действительно, поскольку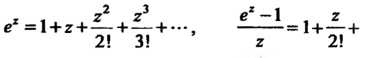
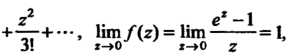 То
То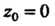 — устранимая особая точка.
— устранимая особая точка.
Пример 37.35. Найти полюсы функции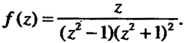
Так как для функции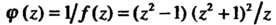 Точки
Точки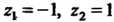 -
-
Нули первого порядка,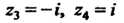 —нули второго порядка, то для функции
—нули второго порядка, то для функции
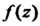 Точки
Точки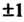 — полюсы первого порядка, точки
— полюсы первого порядка, точки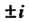 - полюсы второго порядка.
- полюсы второго порядка.
Замечание. Если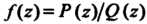 , где
, где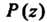 И
И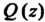 - многочлены,
- многочлены,
Не имеющие общих корней, то корни многочлена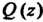 (и только они) являются полюсами функции
(и только они) являются полюсами функции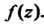 Порядок полюсов
Порядок полюсов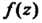 Совпадает с кратностью соот
Совпадает с кратностью соот
Ветствующих корней многочлена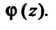 Например, когда
Например, когда
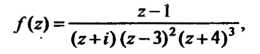
То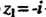 - простой полюс,
- простой полюс,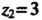 — полюс второго порядка,
— полюс второго порядка, - полюс третьего порядка Пример 37.36. Исследовать особые точки функции
- полюс третьего порядка Пример 37.36. Исследовать особые точки функции
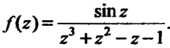
Поскольку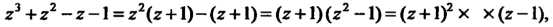
То функция имеет особые точки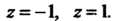 Исследуем точку
Исследуем точку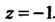 Функцию
Функцию
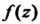 Приведем к виду (37.50):
Приведем к виду (37.50):
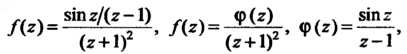
Где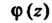 - функция, аналитическая в окрестности точки
- функция, аналитическая в окрестности точки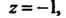 Причем
Причем
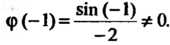 Следовательно, точка
Следовательно, точка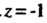 Является полюсом второго порядка. Аналогично, записав функцию
Является полюсом второго порядка. Аналогично, записав функцию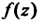 В виде
В виде
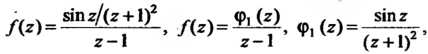
Заключаем, что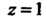 - простой полюс данной функции.
- простой полюс данной функции.
Пример 37.37. Найти особые точки функции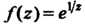 И опреде
И опреде
Лить их типы.
Принимая во внимание, что (см. (37.3))
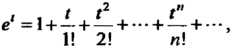
При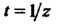 Получим
Получим
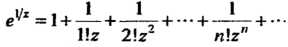
Этот ряд сходится всюду, кроме точки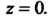 Его можно рассматривать как
Его можно рассматривать как
Разложение функции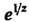 В ряд Лорана в окрестности точки
В ряд Лорана в окрестности точки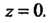 Поскольку
Поскольку
Главная часть ряда имеет бесконечное множество членов, то точка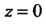 является существенно особой точкой для функции
является существенно особой точкой для функции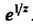
| < Предыдущая | Следующая > |
|---|