37.6. Ряд Тейлора. Ряд Лорана
Функция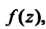
Однозначная и аналитическая в точке
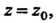Разлагается в ок
Рестности этой точки в ряд Тейлора
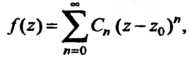(37.37)
Коэффициенты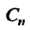
Которого определяются формулами
(37.38)
1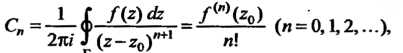
Где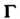
— окружность с центром в точке
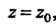, расположенная в окрестности точки
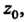В которой функция
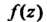Аналитическая. Центр окружности круга сходимости находится в точке
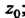; эта окружность проходит через особую точку
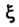Функции 
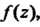Ближайшую к точке
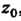, т. е. радиус сходимости ряда (37.37) будет равен расстоянию от точки
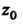До ближайшей особой точки функции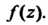
Для функций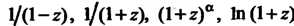
I рады Тейлора имеют
Следующий вид:
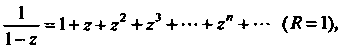(37.39)
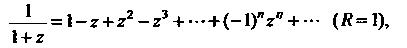(37.40)
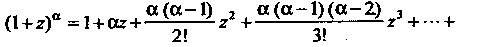
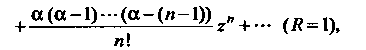(37.41)
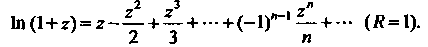(37.42)
Формула (37.42) определяет разложение в рад Тейлора в окрестности точки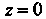 
Главного значения логарифма. Чтобы получить ряд Тейлора для других значений многозначной функции
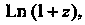Необходимо в правой части добавить
Числа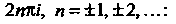
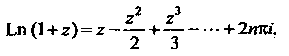
Функция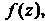
Однозначная и аналитическая в кольце
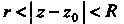(не ис
Ключены случаи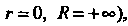
Разлагается в этом кольце в ряд Лорана
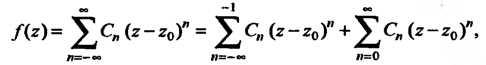(37.43)
Коэффициенты которого определяются формулами
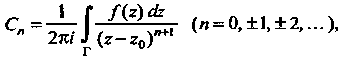(37.44)
Где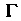
— произвольная окружность с центром в точке
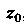, расположенная
Внутри этого кольца.
В формуле (37.43) рад
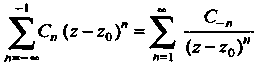
Называется главной частью рада Лорана, а рад
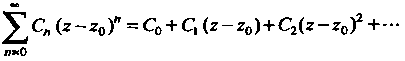
Называется правильной частью рада Лорана.
Пример 37.24. Разложить в ряд Тейлора функцию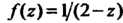
в окрестности точки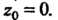
Преобразуем эту функцию следующим образом:
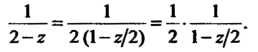
Поскольку (см. формулу (37.39))
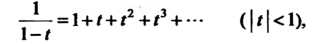(37.45)
То при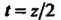
Получим
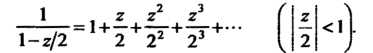
Следовательно,
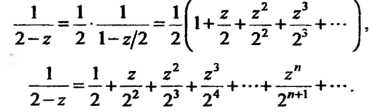
Полученный ряд сходится при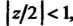
Или
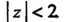
Пример 37.25. Разложить в ряд Тейлора функцию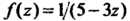
В ок
Рестности точки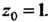
Преобразуем данную функцию:
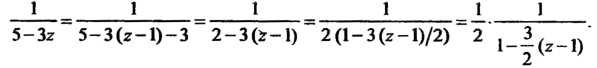
В соответствии с формулой (37.45) при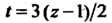
Получаем
Итак,
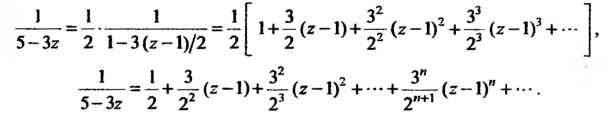
Полученный ряд сходится пр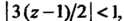и
Или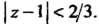
Пример 37.26. Разложить в ряд Тейлора функцию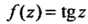
В
Окрестности точки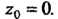
Ближайшая от начала координат особая точка функции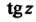
Есть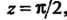
, поэтому
Функция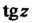
Разлагается в ряд
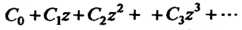В круге
Заметив, что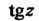
— нечетная функция, поэтому в разложении будут только члены с нечетными показателями, использовав равенство
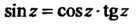И ряды
Для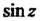
И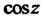
(см. формулы (37.4) и (37.5)), получим
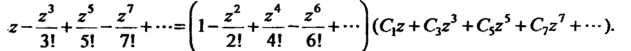
Сравнивая коэффициенты при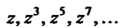
В обеих частях равенства, находим
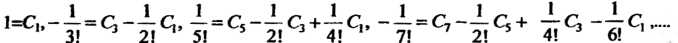
Из этих уравнений определяем коэффициенты: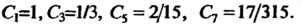
Следовательно,
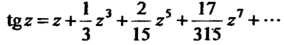(37.46)
Пример 37.27. Найти первые три члена ряда Тейлора по степеням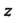
функции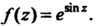
Поскольку (см. формулу (37.3))
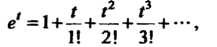
То при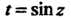
Получим
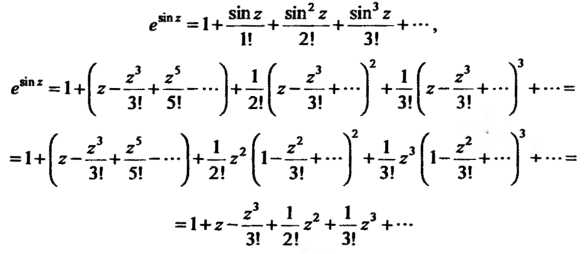
Итак,
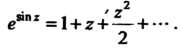
Пример 37.28. Разложить функцию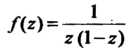
В ряд Лорана в сле
Во всех этих кольцах данная функция является аналитической и поэтому может быть разложена в них в соответствующий ряд Лорана. Представим эту функцию в виде суммы элементарных дробей:
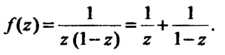
1. Поскольку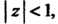
То с учетом формулы (37.39) получим
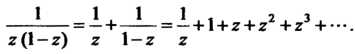
Главная часть ряда Лорана здесь имеет только один член.
2. Если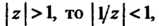
Поэтому
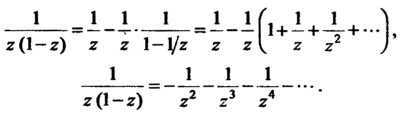
В этом разложении отсутствует правильная часть.
3. Если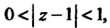
То функцию
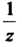Нужно разложить в геометрический ряд со знаменателем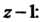
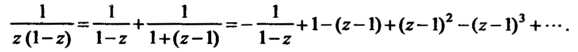
Главная часть полученного ряда Лорана содержит только один член.
Пример 37.29. Функцию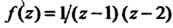
Разложить в ряд Лорана,
Приняв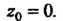
Данная функция имеет две особые точки: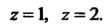
Следовательно, име
Ется три кольца с центром в точке 0, в каждом из которых функция аналитическая: 1) круг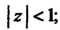
2) кольцо
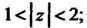3) внешность круга
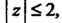Т. е.
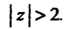
Функцию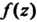
Разлагаем на элементарные дроби:
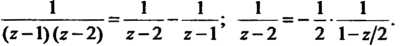
’ 1. Поскольку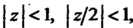
То с учетом (37.39) получим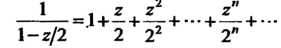 
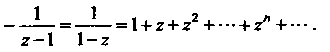(II)
Сложив ряды (I) и (II), найдем, что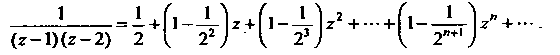 
Полученный ряд является рядом Тейлора.
2. Если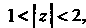
То ряд (I) сходящийся (ибо
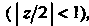, но ряд (II) расходится (так как
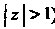|. Разложение (II) заменим другим:
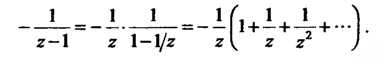(III)
Ряд (III) сходится, поскольку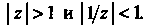
Сложив ряды (I) и (III), получим ряд Лорана для данной функции: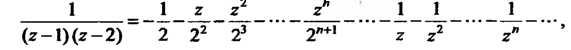 
в котором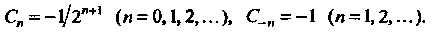
3. Когда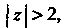
То равенство (III) верно, поскольку и
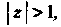Но ряд в правой части формулы (I) уже будет расходящимся. Разложение (I) заменим другим:
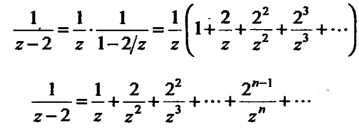(IV)
Этот ряд сходится, так как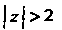
И, следовательно,
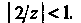Сложив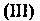
И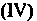
Получим разложение данной функции в ряд Лорана
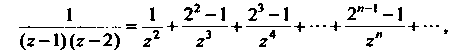
Для которого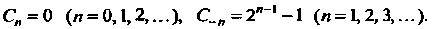
Пример 37.30. Функцию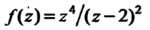
Разложить в ряд
Лорана по степеням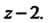
Обозначим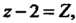
Тогда
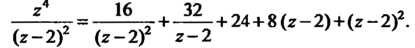
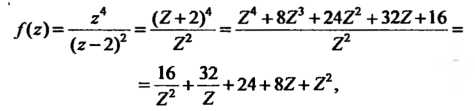
Здесь главная часть ряда Лорана имеет два члена, а правильная - три члена. Поскольку полученное разложение содержит только конечное количество членов, то оно справедлива для любой точки плоскости, кроме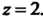
| < Предыдущая | Следующая > |
|---|
