37.5. Интегральная формула Коши

Если функция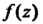Является аналитической в области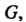Ограниченной кусочно-гладким контуром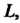И на самом контуре, то верна интегральная формула Коши

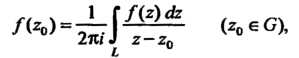(37.33)

Где контур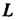Обходится так, чтобы область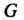Все время оставалась слева (обход контура против часовой стрелки).

Если функция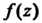Аналитическая в области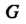И на ее границе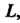То для любого натурального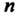Верна формула

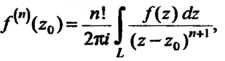(37.34)

Где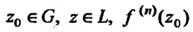- значение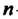-ой производной функции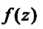В точке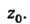

Формулы (37.33) и (37.34) дают возможность вычислить следующие интегралы:

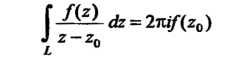(37.35)

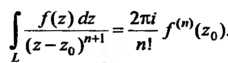(37.36)

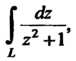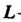Пример 37.20. Вычислить интегралГде-окружность радиуса

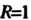С центром в точке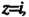Причем обход кошура осуществляется против часовой стрелки. Чтобы воспользоваться формулой (37.35), преобразуем подынтегральную функцию следующим образом: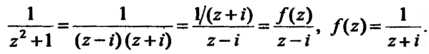

Функция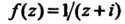Является аналитической внутри рассматриваемого

Круга и на его границе, поэтому справедливы формулы (37.33) и (37.35). В соответствии с последней формулой получаем

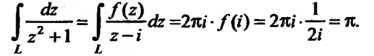
Пример 37.21. Вычислить интеграл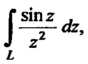Где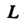-любой замк

Нутый контур, который не проходит через точку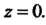Обход контура со

Вершается против часовой стрелки.

Если точка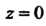Находится вне контура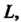То функция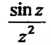Будет аналитической на контуре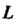И в области, ограниченной этим контуром, поэтому в соответствии с теоремой 37.1 интеграл равен нулю:

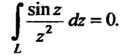
Если точка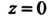Принадлежит области, ограниченной контуром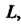То

Справедливыми будут формулы (37.34) и (37.36) для функции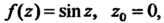

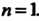На основании формулы (37.36) для этого случая, поскольку 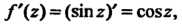Получим

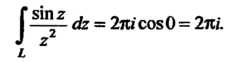
Пример 37.22. Вычислить интеграл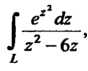Где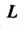-окружность

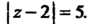
В области, ограниченной окружностью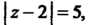Имеются две точки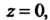

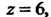В которых знаменатель дроби равен нулю. Формулой (37.33) непосредственно пользоваться нельзя. В этом случае вычислить интеграл можно следующим образом. Разложим дробь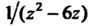На элементарные дроби:

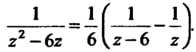
С учетом этого равенства и в соответствии с формулой (37.35) получаем (пр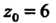и И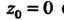Соответственно):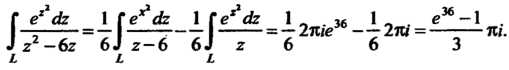

Пример 37.23. Вычислить интеграл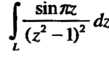Где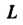- окружность

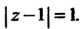
Подынтегральная функция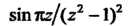Является аналитической в области

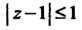Везде, кроме точки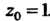. Выделим под знаком интеграла функцию 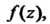аналитическую в круге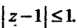Для этого запишем подынтегральную функцию в виде

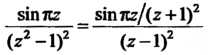
И в качестве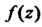Рассмотрим функцию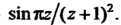

На основании формулы (37.36) при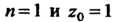Получим

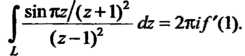
Найдем производную функции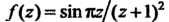И ее значение при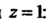

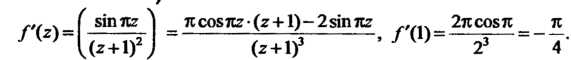
Следовательно,

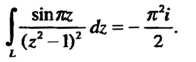
< Предыдущая		Следующая >