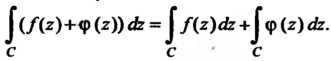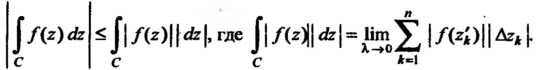37.4. Интегрирование функций комплексной переменной

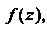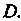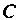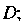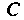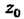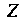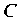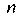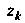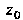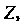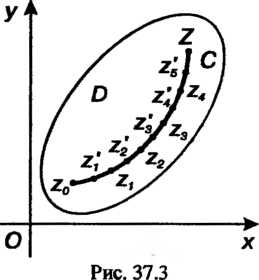
Рассмотрим однозначную функциюОпределенную и непрерывную в области Пусть— кусочно-гладкая дуга линии, которая целиком принадлежит области дугаОграничена точками(начальная) и(конечная). Разделим дугуНа элементарных дуг, занумеруем точки деленияВ направлении от точкиДо конечной точкиПричем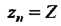(рис. 37.3,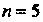). Введем обозначения: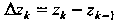

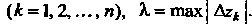На каждой элементарной дуге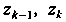Выберем одну

Точку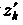(один из концов или внутреннюю точку) и запишем сумму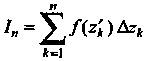

Интегралом от функции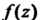По дуге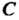Называется конечный предел суммы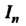При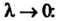

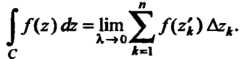
Интеграл от функции комплексной переменной имеет следующие свойства:

1.

2.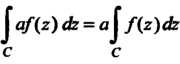(а — постоянная).

3.  Если дуга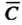Геометрически совпадает с дугой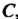, но имеет направление, противоположное направлению дуги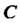(для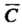Начальная точка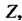А конечная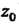), то

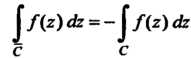
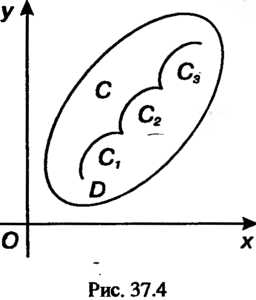
4.  Если дуга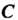Состоит из дуг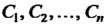(рис. 37.4,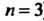), то

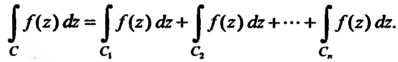
5.

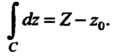
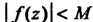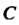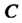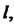6.  ЕслиВо всех точках дугиИ длина дугиРавнаТо

?.

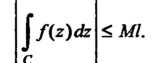
Вычисление интеграла от однозначной функции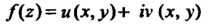 комплексной переменной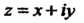Сводится к вычислению обычных криволинейных

Интегралов:

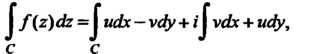(37.27)

Где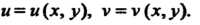

От пути интегрирования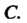

Если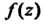— аналитическая функция в односвязной области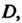То значение интеграла

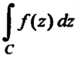Не зависит от линии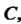А только от

Начальной и конечной точки этой линии.

Теорема 37.1 (Коши). Для всякой функции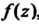, аналитической в некоторой односвязной области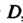, интеграл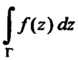По любому замкнутому кусочно-гладкому контуру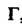, целиком принадлежащему области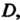Равен нулю:

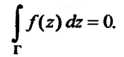
Если кривая С задана параметрическими уравнениями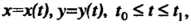То

(37.28)

Где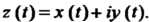

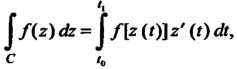
Если функция /(г) аналитическая в однозначной области Д содержащей точк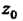иИ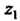, то справедлива формула Ньютона-Лейбница

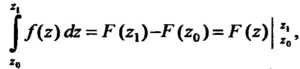(37.29)

Где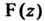- первообразная для функции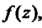Т. е.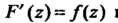А области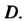

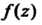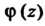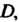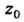Если функцииИ- аналитические в односвязной областиАИ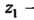 произвольные точки этой области, то справедлива формула интегрирования по частям:

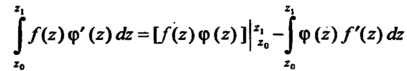(37.30)

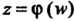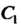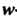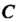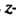Замена переменной в интегралах от функций комплексной переменной проводится аналогично случаю функции действительной переменной. Если аналитическая функцияОтображает взаимно однозначно линиюВ-плоскости на линиюВПлоскости, то

Если путь интегрирования является лучом, исходящим из точки z0 или окружностью с центром в точке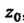, то целесообразна подстановка

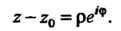(37.32)

В первом случае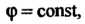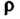-действительная переменная интегрирования, во

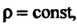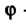Втором случаеА- действительная переменная интегрирования.

Пример 37.15.Вычислить интеграл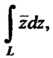Где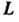-линия, соединяю

Щая точки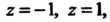Причем: 1)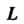-отрезок действительной оси от точки

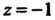До точки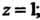2)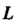- верхняя полуокружность 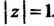Поскольку для комплексного числа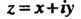Сопряженным является число

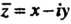, то надействигельной ос»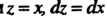И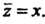В первом случае получаем

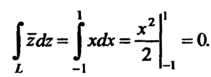
Верхнюю полуокружность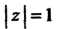Можно задать так: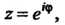Где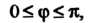

Причем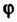Убывает. Поскольку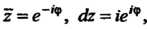То во втором случае

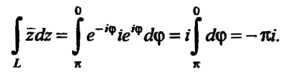
Замечание. Функция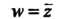Не является аналитической (для

Функций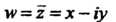Не выполняются условия (37.25)); значение интегра

Ла от этой функции зависит от пути интегрирования, соединяющего указанные точки.

Пример 37.16. Вычислить интеграл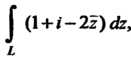Где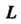- отре-зок

Прямой между точками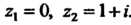

Перепишем подынтегральную функцию в виде (37.1)

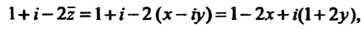
Здесь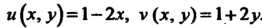

На основании формулы (37.27) получаем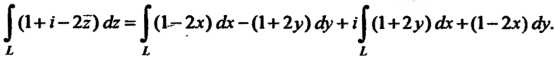

Отрезок прямой между точками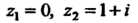Имеет уравнение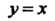

I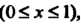Поэтому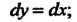Пределы интегрирования соответственно равны:

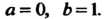Следовательно,

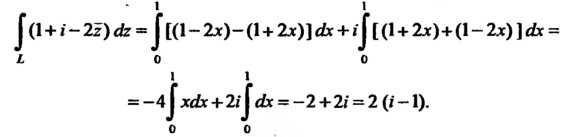
Пример 37.17.Вычислить интегралгде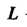-окружность ра

Диуса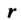С центром в точке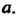

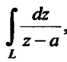
Переходим к новой переменной в соответствии с формулой (37.32): 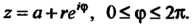На основании формулы (37.31) получаем

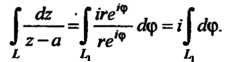
Поскольку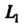- отрезок действительной оси от точки 0 до точки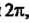То

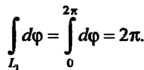
Таким образом,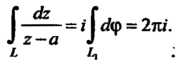

Пример 37.18. Вычислить интеграл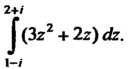

Поскольку подынтегральная функция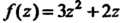Является аналитической

Везде, то с помощью формулы Ньютона-Лейбница находим:

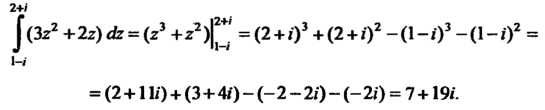
Пример 37.19. Вычислить интеграл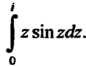

Функция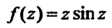Является аналитической на всей плоскости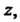Поэтому ин

Теграл от нее не зависит от пути интегрирования, соединяющего точк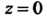иИ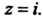

На основании формулы интегрирования по частям (37.30) и формулы Ньютона-Лейбница получаем

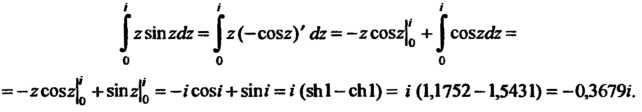
Замечание. Здесь использованы равенства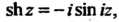 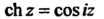При ”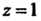(см. формулы (37.12)):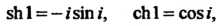

Поэтому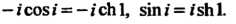

< Предыдущая		Следующая >