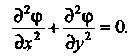37.3. Дифференцирование функций комплексной переменной

Рассмотрим функцию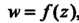, определенную в некоторой области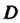Ком

Плексной плоскости, и точки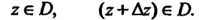Обозначим:

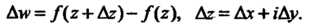
Производной функции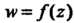В точке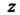Называется конечный предел отно

Шения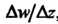, когда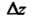Произвольным образом стремится к нулю:

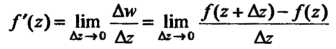(37.24)

Функция, имеющая производную в точке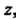, называется дифференцируемой в этой точке.

Если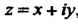,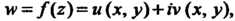То в каждой точке дифференци

Руемое™ функции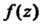Выполняются равенства

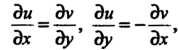(37.25)

Которые называют условиями Д’Аламбера—Эйлера (или условиями Коши - Римана).

Обратно, если в некоторой точке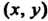Функции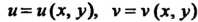Диф

Ференцируемы как функции действительных переменных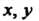И, кроме того, удовлетворяют соотношениям (37.25), то функция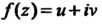Является дифференцируемой в этой точке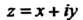Как функция комплексной переменной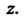

Функция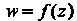Называется аналитической в точке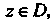Если она диффе

Ренцируема в ней и некоторой ее окрестности. Функция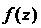Называется аналитической в области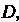, если она дифференцируема в каждой ее точке.

Для всякой аналитической функции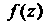Производная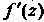Выражается че

Рез частные производные функций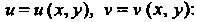

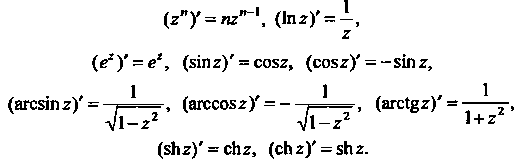
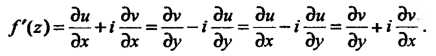
Геометрический смысл модуля и аргумента производной. Если функция 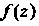- аналитическая в точке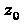И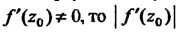Равен коэффициенту рас

Тяжения в точке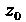При отображении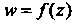Плоскости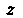На плоскость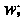Точ

Нее: при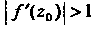Будет растяжение, а при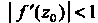- сжатие. Аргумент про

Изводной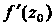Равен углу, на который необходимо повернуть касательную в точке

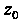К любой гладкой кривой на плоскости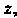Которая проходит через точку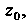Чтобы получить направление касательной в точке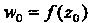К образу этой кривой на плоскости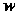При отображении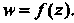Отметим, что при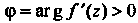Поворот осуществляется против часовой стрелки, а при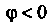- по часовой стрелке.

Отображение с помощью аналитической функции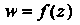Называется

Конформным отображением.

Диффереицироваиие элементарных функций. Производные элементарных функций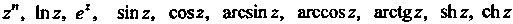Находят

Ся по формулам:

Гармоническая функция. Функция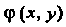Называется гармонической в об

Ласти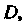Если она имеет в ней непрерывные частные производные второго порядка и удовлетворяет в этой области уравнению Лапласа

(37.26)

Если функция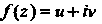Аналитическая в области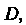То ее действительная

Часть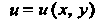Й мнимая часть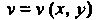Являются гармоническими

Функциями в этой области.

Однако, если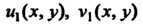— две произвольные гармонические функции, то

Функция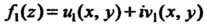Вовсе не обязана быть аналитической функци

Ей: для аналитичности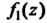Нужно, чтобы функции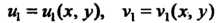

Удовлетворяли условиям Д’Аламбера — Эйлера.

Пример 37.9. Выяснить, является ли аналитической функция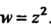 Поскольку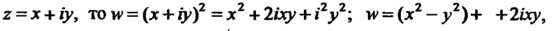

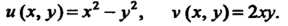Находим частные производные функций

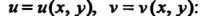
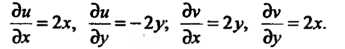
Следовательно,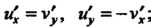; условия (37.25) выполнены для всех точек плос

Кости Оху. Значит, функция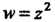Является аналитической на всей плоскости.

Пример 37.10. Выяснить, является ли аналитической функция w = z. Если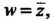То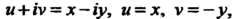Откуда

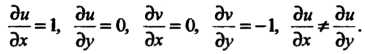
Следовательно, первое из условий (37.25) не выполняется. Функция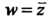Не имеет

Производной ни в одной точке плоскости и поэтому не является аналитической. Пример 37.11. Выяснить, является ли аналитической функция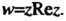 Если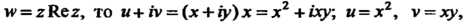Откуда

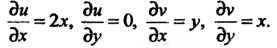
Равенства (37.25) выполняются только при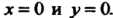Таким образом, функция

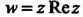Дифференцируема только в точке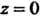И нигде не является аналитической. Пример 37.12. Найти аналитическую функцию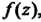Если известна ее

Мнимая часть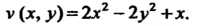 Поскольку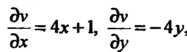

То из равенств (37.25) получаем

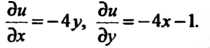
Из первого уравнения находим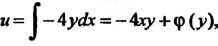Где-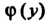

Произвольная функция. Для определения функции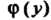Продифференцируем по

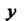Функцию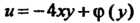И подставим полученную производную во второе

Уравнение: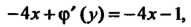Откуда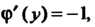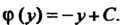Следова-

Тельно,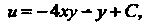Поэтому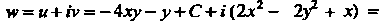

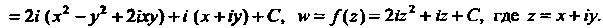
Пример 37.13. Найти аналитическую функцию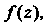Если ее

Действительная часть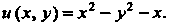 Так как

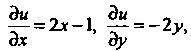
То из равенств (37.25) следует, что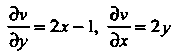

Из первого уравнения находим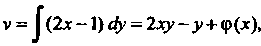Где-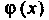

Произвольная функция. Для определения функции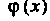Находим

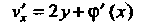И подставляем во второе уравнение: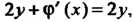Откуда

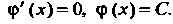Значит,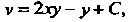Поэтому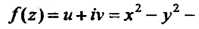

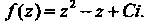
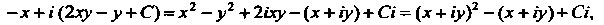
Пример 37.14. При каком условии трехчлен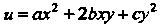Являет

Ся гармонической функцией?

Находим частные производные первого и второго порядка: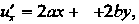

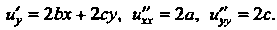Вторые частные производные удовлетворяют уравнению (37.26), т. е.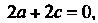Когда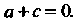При этом условии данный

Трехчлен будет гармонической функцией.

< Предыдущая		Следующая >