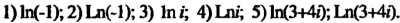37.2. Основные элементарные функции комплексной переменной

Функции комплексной переменной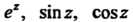Определяются как суммы соот

Ветствующих степенных рядов, сходящихся на всей комплексной плоскости:

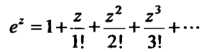(37.3)

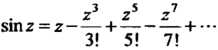(37.4)

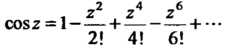(37.5)

Показательная функция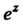Имеет следующие свойства: 1)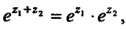Где

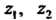- произвольные комплексные числа; 2)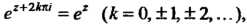Т. е.

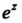Является периодической функцией с периодом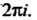

Тригонометрические функции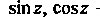-периодические с действительным

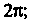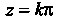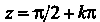ПериодомОни имеют только действительные нулиИСо

Ответственно, где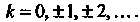

Для функций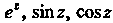Справедливы формулы Эйлера

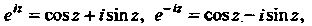(37.6)

Откуда

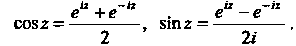(37.7)

Если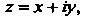То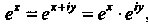, поэтому

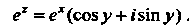(37.8)

Тригонометрические функцииОпределяются формулами

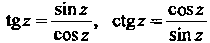
Все формулы тригонометрии остаются справедливыми и для тригонометрических функций комплексной переменной.

Гиперболические функции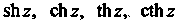Определяются формулами:

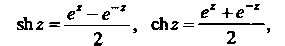(37.9)

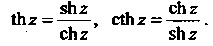(37.10)

Функции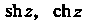Можно рассматривать как суммы степенных радов, сходя

Щихся на всей комплексной плоскости:

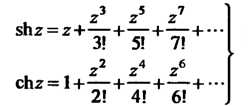(37.11)

Тригонометрические и гиперболические функции связаны между собой следующими равенствами:

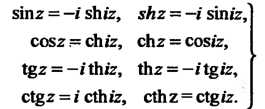(37.12)

Логарифмическая функция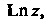Где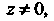Определяется как функция, обрат

Ная показательной, причем

Эта функция является многозначной. Главным значением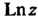Называется такое значение, которое получается при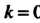>; оно обозначается через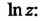

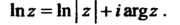(37.14)

Очевидно, что

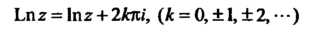(37.15)

Справедливы следующие равенства:

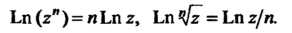
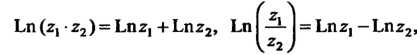
Обратные тригонометрические функции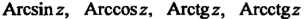 определяются как функции, обратные соответственно функциям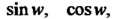

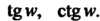Например, когда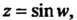То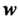Называется арксинусом числа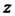И

Обозначается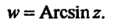

Все эти функции являются многозначными; они выражаются через логарифмические функции следующими формулами:

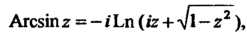(37.16)

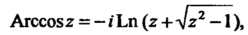(37.17)

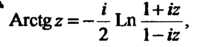(37.18)

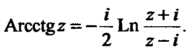(37.19)

Главные значения обратных тригонометрических функций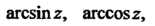

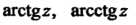Получаются, когда рассматриваются главные значения соответствующих логарифмических функций.

Общая степенная функция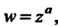Где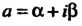- любое комплексное число,

Определяется формулой

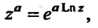(37.20)

Ее главное значение равно

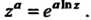(37.21)

Общая показательная функция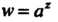(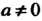- любое комплексное число) оп

Ределяется формулой

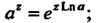(37.22)

Главное значение этой многозначной функции равно

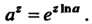(37.23)

Пример 37.4. Доказать, чт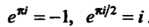о Число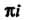Можно рассматривать как комплексное число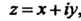, где

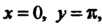Поэтому в соответствии с первой из формул (37.6) находим

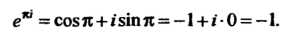
Аналогично получаем второе равенство:

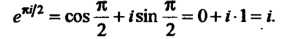
Пример 37.5. Найти: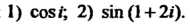

По первой из формул (37.7) получаем

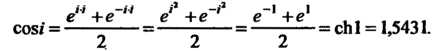
В соответствии со второй из формул (37.7) находим:

Пример 37.6. Найти:

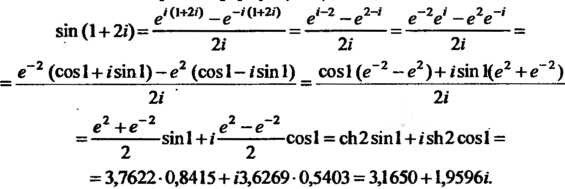
Поскольку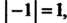А главное значение аргумента равно, то в соответствии с

Формулой (37.14) получим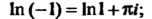По формуле (37.15) найдем:

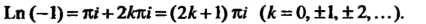
На основании тех же формул и с учетом того, что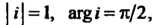Находим

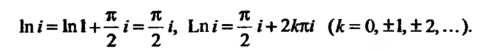
Так как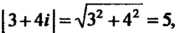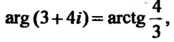То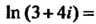

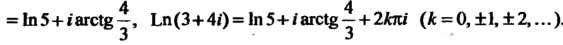
П р и м е р 37.7. Найти: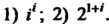

В соответствии с формулой (37.20) или (37.22) при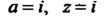И с учетом то

Го, что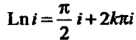(см. пример 37.6) получаем

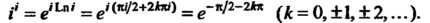
Главное значение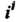Равно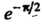

На основании формулы (37.22) при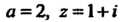Находим:

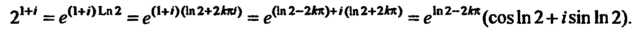
Замечание. Здесь использована формула (37.8).

Пример 37.8.Найти: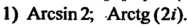

С помощью формул (37.13) и (37.16) находим

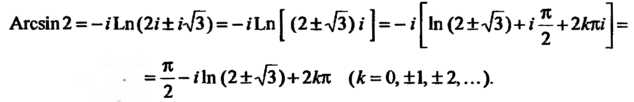
В соответствии с формулами (37.13) и (37.18) получаем

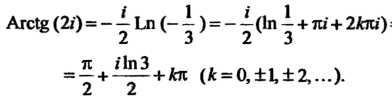
< Предыдущая		Следующая >