37.1. Понятие функции комплексной переменной. Предел и непрерывность

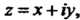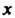Комплексное числоГдеИ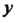- действительные числа,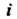- мнимая

Единица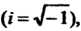Изображается точкой комплексной плоскости с координатами

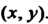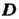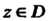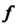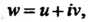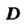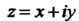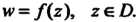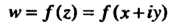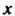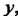Пусть- область (открытое связное множество) комплексной плоскости С. Если каждой точкеПо определенному правилуПоставлено в соответствие единственное комплексное числоТо говорят, что в области определена однозначная функция комплексной переменнойИ пишут ФункциюМожно рассматривать как комплексную функцию двух действительных переменныхИ, определенную в области D. Задание такой функции равносильно заданию двух действительных функций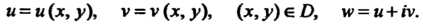Таким образом, если 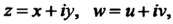То

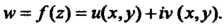(37.1)

Комплексное число с называется пределом однозначной функци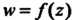и При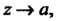Если для всякого числа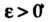Существует такое число

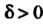, что из неравенства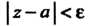Следует неравенство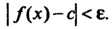

В этом случае пишут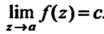

Функция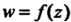Называется непрерывной в точке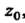, если

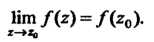
Функция, непрерывная в каждой точке некоторой области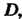Называется непрерывной в этой области.

Область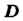Называется односвязной, когда она ограничена замкнутой линией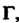Не пересекающей себя (рис. 37.1). Область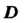Называется двусвязной, когда она ограничена двумя замкнутыми линиям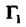иИ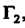, которые не пересекаются и каждая не пересекает себя (рис. 37.2); внутренняя линия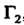, в частности, может вырождаться в точку или в дугу непрерывной линии. Аналогично определяется трехсвязная, четырехсвязная и т. д. области.

Замечание. Если существуют значения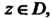Каждому из которых постав

Лены в соответствие несколько значений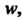То функция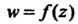Называется много

Значной.

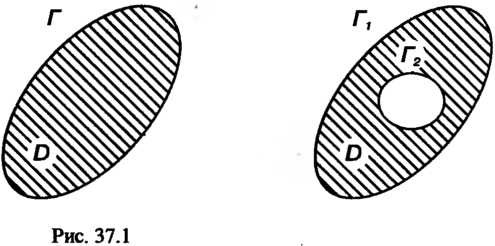
Пример 37.1. Найти значения функции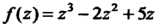При сле

Дующих значениях аргумента: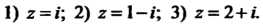

Принимая во внимание значения степеней мнимой единицы (см. формулы (7.19)), получаем: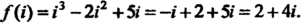Поскольку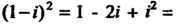

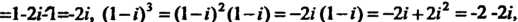То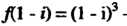

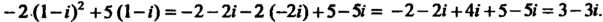Далее,

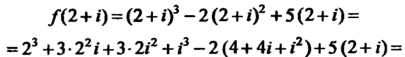
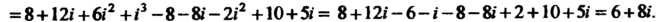
Пример 37.2. Дана функция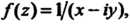Где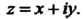Найти ее

Значения при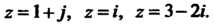

Сначала придадим функции вид (37.1):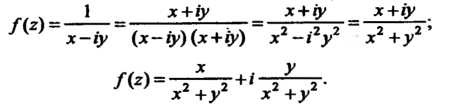

При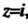, это значит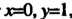.получим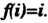В случае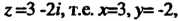Находим

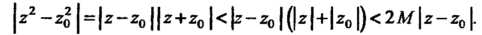
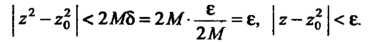
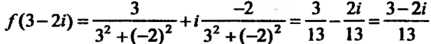
Замечание. Данную функцию можно записать и в таком виде: 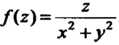. С учетом этой формулы находим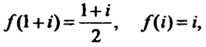

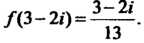
Пример 37.3. Доказать, что функция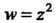Является непрерывной при

Любом значении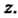

Зафиксируем значение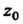И рассмотрим разность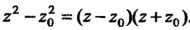. Ко

Гда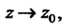То существует такое положительное число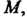При котором выполня

Ются неравенства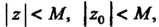Поэтому

Выберем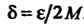. Из неравенства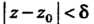Следует, что

Следовательно,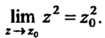Поскольку выполняется равенство (37.2), то функция

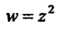Непрерывна в точке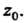Точка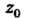Была зафиксирована произвольно; значит, функция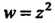Непрерывна в любой точке.

< Предыдущая		Следующая >