36.5. Эмпирические формулы

Во многих науках (физика, химия, технические науки и др.) приходится пользоваться эмпирическими формулами, составленными на основании результатов наблюдений. Параметры эмпирических формул определяются по способу наименьших квадратов. Сначала устанавливается вид зависимости между двумя величинами. Это можно выполнить разными способами, например графически. Пусть результаты измерений представлены схемой

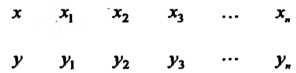
Упорядоченные пары чисел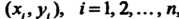, рассматриваются как прямоугольные декартовы координаты точек  на плоскости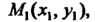

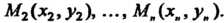В выбранной  системе координат строят

Точки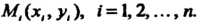

Если построенные точки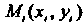Незначительно уклоняются от некоторой прямой,

То полагают, что между величинами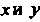Существует линейная зависимость, т. е.

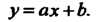(36.30)

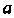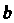ПараметрыИЭмпирической формулы (36.30) определяются из системы уравнений

(36.31)

Если точки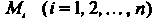Незначительно уклоняются от дуги некоторой

Параболы, то естественно предположить, что между величинам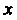иИ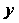Существует квадратичная зависимость, т. е.

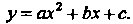(36.32)

Параметры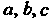Эмпирической формулы (36.32) определяются из системы уравнений

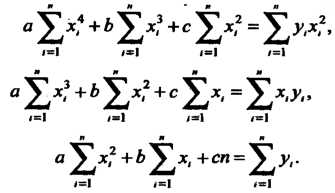(36.33)

Пример 36.3. Экспериментально получены пять значений искомой функции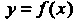При пяти значениях аргумента:

Методом наименьших квадратов найти функцию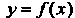В виде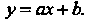

Результаты измерений и их обработки запишем в табл. 36.2.

Таблица 36.2.

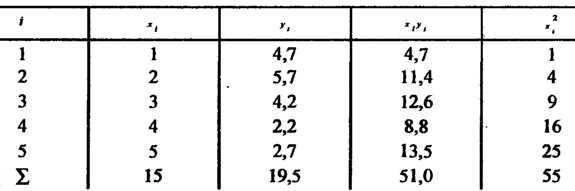
Система уравнений (36.31) принимает вид

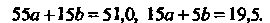
Решая эту систему, находим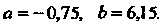Следовательно, получена эмпи

Рическая формула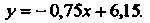

VII ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ И ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ

Гпава 37

ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ

< Предыдущая		Следующая >