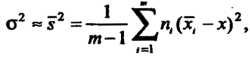36.4. Оценки точности измерений
Предполагается, что измерения являются независимыми и равноточными (с одной и той же дисперсией), а их погрешности - случайными, причем распределены они по нормальному закону. В качестве показателя точности измерений оценивается
Дисперсия этого закона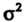 Или средняя квадратическая погрешность
Или средняя квадратическая погрешность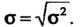
Точечные оценки днсперснн. 1. Если измеряют известную величину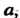 То в качестве эффективной оценки дисперсии
То в качестве эффективной оценки дисперсии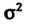 Применяют квадрат среднего квадратического отклонения
Применяют квадрат среднего квадратического отклонения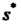 Результатов измерений (36.13) от значения
Результатов измерений (36.13) от значения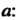
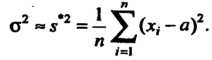 (36.25)
(36.25)
2. При измерениях неизвестной величины в качестве оценки дисперсии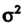 применяют эмпирическую дисперсию
применяют эмпирическую дисперсию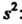
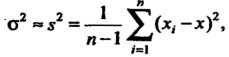 (36.26)
(36.26)
Где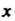 - среднее арифметическое значений
- среднее арифметическое значений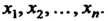 Оценка (36.26) является
Оценка (36.26) является
Несмещенной и состоятельной, но не является эффективной (она асимптотически
Эффективна, т. е. ее дисперсия стремится к наименьшему значению при неограниченном увеличении числа измерений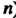 |.
|.
3. Если проводится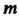 Серий измерений некоторой величины и известны количества измерений
Серий измерений некоторой величины и известны количества измерений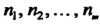 , а также средние арифметические результаты
, а также средние арифметические результаты 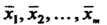 В каждой серии, то в качестве оценки дисперсии применяют эмпирическую дисперсию
В каждой серии, то в качестве оценки дисперсии применяют эмпирическую дисперсию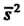 Из средних:
Из средних:
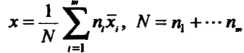 (36.28)
(36.28)
Эта оценка является несмещенной, состоятельной (и асимптотически эффективной при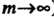 ).
).
Доверительные оценки средней квадратической погрешности. При большом числе измерений доверительную оценку средней квадратической погрешности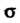 Записывают в виде оценки относительного отклонения оцениваемого значения
Записывают в виде оценки относительного отклонения оцениваемого значения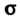 От эмпирического стандарта
От эмпирического стандарта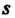 (или
(или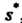 , или
, или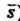 ). Эта оценка имеет вид
). Эта оценка имеет вид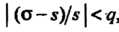 , или
, или
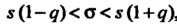 (36.29)
(36.29)
Коэффициент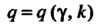 Находится с помощью соответствующих таблиц в зави
Находится с помощью соответствующих таблиц в зави
Симости от доверительной вероятности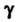 (надежности оценки) и от числа степеней свободы
(надежности оценки) и от числа степеней свободы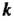 (
(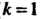 В случае 1,
В случае 1,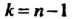 В случае 2,
В случае 2,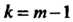 В случае 3).
В случае 3).
При малом числе измерений симметричная оценка (36.29) приводит к неоправданно большим доверительным интервалам; в этом случае применяют асимметричные доверительные оценки вида,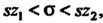 Где
Где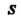 - эмпирический стандарт; значения коэффициентов
- эмпирический стандарт; значения коэффициентов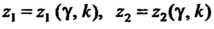 Находятся по таблицам.
Находятся по таблицам.
| < Предыдущая | Следующая > |
|---|